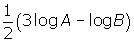Learning Resources

Lesson

From our previous work, we know that logarithms are actually exponents. We would therefore expect the properties and laws of exponents to be reflected in the properties and laws of logarithms. The following numerical example should help you understand the rule you are asked to discover in Step A of Investigation 13 on page 176 of your text.

The law of logarithms for a quotient of two numbers is left to you to discover in Step B of the Investigation. The logarithm of a power, which you are asked to discover in Step C of the investigation, is developed using a numerical example in the interactive below.

Complete Investigation 13 on page 176 of your text before you proceed to the next part of this lesson.

If you have completed Investigation 13 you should have discovered the three laws of logarithms that are summarized below:

1. Product Law of Logarithms:   
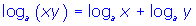
2. Quotient Law of Logarithms:  
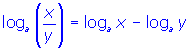
3. Power Law of Logarithms:      

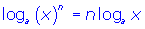
Study the following examples to see how these laws can be used in various ways to simplify expressions and solve problems.

Example

Use the laws of logarithms to write each of the following expressions as a single logarithm:

(a) log 7 + log 8                 (b) log₃ 48 - log₃ 24        (c) log₂ 3⁵

Solution

(a)  log 7 + log 8  = log (7 x 8) = log 56
       (Check this on your calculator by finding log 7 and log 8 and adding. Then
         compare the answer to log 56)

(b)  log₃ 48 - log₃ 24 = log₃ (48 ¸ 24) = log₃ 2

(c)  log₂ 3⁵ = 5 log₂ 3

Example

Use the laws of logarithms to write the following expression as a single logarithm:  4 log 2 + log 3 - log 12

Solution

 

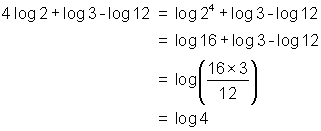
We can solve equations which contain logarithmic expressions by first converting them to exponential equations. If possible, we then write the expression on each side of the equal sign as a power to the same base and use the techniques we learned earlier in this unit. An example of this is shown below:

Example

Solve for x the equation:  log₂ 32 = 3x

Solution

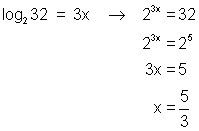
However, sometimes when we convert the equation to the exponential form we cannot write the expressions on both sides to the same base. We then have to use a different approach to solving the exponential equation part of the problem. An example of this is shown below.

Example

Solve for x the equation: 2^x = 12

Solution

We know that x lies between 3 and 4 because 2³ = 8 and 2⁴ = 16. To find the value of x, take the logarithm to base 10 of the expressions on both sides of the equation. This gives the following:

Check the solution obtained in the interactive above by entering 2^3.585 into your calculator. You will discover that although it is not exactly equal to 12 it is very close. You should check all your solutions to exponential equations in this way.

Activity

1. Complete Investigation 13 on page 176 in your text.
2. Complete the Investigation Questions 1 - 6 on pages 177 & 178.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Solve for x: 
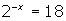
2. Write as a single logarithm: 

Solution