Learning Resources

Outcomes

In this lesson you will

• Discover a way to solve for x in equations like 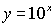by using a graph and/or guess-and-check method.
• Discover that the log button on the calculator reverses the process of exponentiation.
• Be introduced to the terminology associated with logarithms.
• Be formally introduced to the concept of the inverse of a function and recognize that logarithmic functions are inverses of exponential functions.

By the end of this section you should be able to:

• Demonstrate an understanding, algebraically and graphically, that the inverse of an exponential function is a logarithmic function.
• Demonstrate an understanding of the role of real numbers in exponential and logarithmic expressions and equations.
• Demonstrate an understanding of the relationships that exist between arithmetic operations and operations used when solving equations.
• Apply real number exponents in expressions and equations.
• Model real-world phenomena using exponential functions.

Introduction

In this section you will discover how to solve, to a large degree of accuracy, for x in an equation like y = 10^x . You will also be connecting the solution to this type of an equation with the concept of a logarithm. You will see how the logarithmic function is the inverse of the exponential function. You will explore the graphs of logarithmic and exponential functions and see how one is a reflection of the other in the line .

Prerequisites

To be successful in this lesson, it would be helpful to know the following:

• How to solve exponential functions by converting powers to the same base.
• How to determine the equation of exponential functions without using technology.
• The meaning of zero, negative, and rational exponents.