Learning Resources

Lesson

In the exponential functions we have studied so far, we have concentrated on exponents that are integers, i.e. {..., -3 , -2 , - 1 , 0 , 1 , 2 , 3 , ...}. There we learned that

However, when we use the TI83 to graph exponential functions, the graphs have been continuous with points between the integral values for x. In other words, we drew the graphs as continuous curves and not as discrete points. This implies that a base can be raised to a power which is not an integer.

Investigation 12 requires you to use your TI83 to explore this possibility and develops the relation between rational exponents and radicals. The tables for STEP A of the Investigation are shown below:

If you want to see the keystrokes necessary to get these tables click here.

Complete Investigation 12 on page 163 in your text now before continuing.

Hopefully you have completed Investigation 12. If you have, you should have discovered the following:

• A base raised to exponent ½ is equivalent to taking the square root of the base. Symbolically this is stated as:

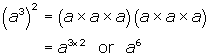
• A base raised to exponent a is equivalent to taking the cube root of the base. Symbolically this is stated as:

Some examples of the above relation are given below:

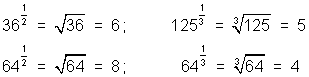
We can use the power of a power rule we learned earlier (which stated that (x^a)^b  = x^ab ) to help define any rational exponent.  An example to illustrate this is shown below:

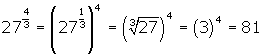
In general, we can state the following relation between rational exponents and radicals:

Some examples of this are given below:

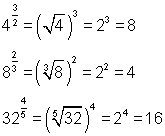
To deal with negative rational exponents, we can apply the power of a power rule and the above definition together. For example, we can simplify 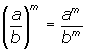as follows:

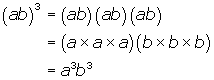
or

Example 1

             Simplify: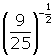  

Solution     

                 

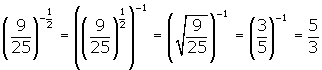
Example 2   

               Solve for x:  

Solution

Example 3

When a painkiller enters the bloodstream, it gradually dilutes, decreasing exponentially with a half-life of 2 hours. If a 100 mg tablet is taken at 4 P.M. at what time will 12.5 mg of the painkiller be still in the bloodstream?

Solution

 Let y represent the quantity remaining after x hours. Then the equation is the general exponential equation which describes the relationship between x and y. 

In this form, a represents the initial value present, thus  a = 100. Also, in this form, b represents the common ratio, which because we are talking about half-life is ½.,  thus b = ½ . Finally, c in the equation represents the change required in the independent variable to produce the common ratio, thus c =2.

The equation is thus:

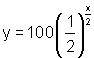
We now substitute 12.5 in for y and solve for x. This is shown in the following interactive.

Activity

1. Complete Investigation 12 on page 163 in your text.
2. Complete the Investigation Questions 1 to 5 on page 164.
3. Do the CYU Questions 6 - 19 on pages 164 - 166.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Evaluate the following without using technology:
     (a)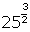              (b)
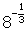
2. Solve for x:   
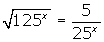
3. Using the formula 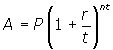( as described in question 18, p.166), answer the following question: If you invest $1000 at 4% interest, compounded quarterly, how much money will you have after 2 years?

Solution