Learning Resources

Lesson

PART 1

This part of Focus F shows how a given number can be expressed as a power of different bases. This skill of expressing a number to different bases will be used to solve exponential equations in Part 2 of this Focus, so it is important that you understand the concept.

As an example, consider the number 16.  

Since 16 = 4 x 4, we can write .

also, since 16 = 2 x 2 x 2 x 2. we can write . 

As well, we know that 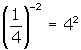, so we can also write . 

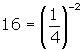For many of the  examples, it is necessary for you to use the Power of a Power rule which states:

Several examples of using this rule given in your textbook on page 157. Study them closely before you proceed to the next part of this lesson.

PART 2

This part of Focus F introduces you to solving exponential equations. In it we will use both graphing and algebraic techniques to solve equations where the variable to be solved for is in the exponent of the expression. This topic is best explained by use of examples.

Example

Solve the exponential equation: 3 = 2^3x - 5

Solution 1

To solve the above equation using algebraic techniques we have to use the skills developed in the first part of this lesson, viz. writing numbers as powers to different bases. The key steps in solving by this method are:

• express both sides of the equation as powers of the same base.
• use the fact that 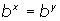if and only x = y (i.e. when the bases are equal, the exponents are equal).

 We will now use this to solve the above example:

Solution 2

Sometimes it is necessary change the base of the numbers on both sides of the equal sign. Although this is a little more involved, the procedure is basically the same. This is shown in the following example.

Example

Solve the equation:   27^2x = (81)^{x - 1}

Solution

There is one last example before you are asked to try some of these problems on your own. It further highlights the connection between equations and functions.

Example

For the function f(x) = 8^2x-5   find:   (i) f(2),   (ii) x when f(x) = ¼

Solution

(i)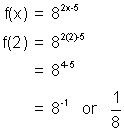              

(ii) This solution is shown in the interactive below:

 

Activity

1. Complete Focus F Parts 1 &2 on pages 157 & 158 in your text.
2. Complete the Focus Questions 8 - 10 on pages 158 & 159.
3. Do the CYU Questions 11 - 19 on pages 159 - 161.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Find the zeros of the function :

Solution