Learning Resources

Lesson

In the previous lessons we explored exponential functions of the type y = ab^x . There we noted that a gives the focal point or y-intercept of the graph. For real-world growth and decay problems a also represents the starting or initial value for the data (since the equation becomes y = a when time = 0) . We also noted that the value of b is the common ratio for equal increments of x.

Investigation 7

What follows are some notes you may wish to refer to as you are working on this investigation.

For Step A in the Investigation, the table can be expanded by using the common ratio, which can be found by taking the ratio of any two successive terms. Once you find the common ratio, multiply the last term in the table by it to get the next term and continue the process to find the remaining terms. Round the common ratio to two places after the decimal for ease of working.

For Step B, you should be able to write the equation without using technology. The equation will have the form y = ab^x , and you found the value of b in Step A. The initial value, a,  is given in the table at time zero and is1.50. Substitute these in and you have the equation. To check, you can do an exponential regression on your TI83 calculator. However, this is only a check. You are expected to be able to find these equations without using technology.

For Step C,  look at the table you completed in Step A and see at what time the value of the car doubles (i.e. becomes 150 x 2 or 300).  Now look at each of the equations given and see if substituting in the time at which the value doubles gives the equation y = 150 x 2. In other words, the doubling time substituted into the equation must make the exponent of the base equal to 1. Test all the equations till you find the right one.

For Step D, the procedure is the same as for Step C, except your will find from the table the time at which the value quadruples (i.e. y = 150 x 4 or 600). Note the base in these equations is 4, whereas the base for Step C was 2.

Investigation 7 showed that the same table of values can be modeled by different looking exponential functions. This is accomplished by using different time periods to determine the common ratio. The different time period changes the base of the function and to compensate for this change the exponent then has to be operated upon in order for the equation to model the data. 

The example below, like the one in Investigation 7, demonstrates how to use these different bases.

Example

If a certain strain of bacteria grows according to the following table, find an exponential equation to describe it. Write the exponential equation based on:

• a  time difference of 1 minute
• the doubling time
• the quadrupling time.

Time (min)	0	1	2	3	4	5	6
Number of bacteria	100	126	159	200	252	317	400

Solution

A time difference of 1 minute

The common ratio for equal 1 minute increments of x can be found by looking at any two consecutive y-values which gives: 

The initial value is 100. Therefore, for , we have a = 100 and b = 1.26. This gives the function

The doubling time

From the table, the doubling time in minutes is 3. For doubling time the common ratio is 2, which means b = 2, with the initial amount still the same, i.e. a = 100. We substitute these into the equation but we must ensure that the exponent at 3 minutes is 1 in order to guarantee the number of bacteria to be 200. We must also ensure the exponent at 6 minutes is 2 to guarantee 400 bacteria. Since and , we can write:

 

The quadrupling time

Using the same argument for quadrupling, the base is 4. Since the number of bacteria quadruples in 6 minutes, the exponent at that time has to be 1. Thus the exponent will be , which gives the function:

Summary

All three of the above equations models the data in the table. Check this by substituting x = 4 into each of them and comparing the answers. 

Note that the initial value a does not change regardless of which base is used. However, by changing the base, the independent variable x has to be operated on to reflect that change. 

The equation takes the form , where c is the time interval required for the common ratio to occur. For the above example this can be interpreted as:

• the number of bacteria increases by a factor of 1.26 for every minute (c = 1): 
                                   

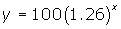
• the number of bacteria increases by a factor of 2 for every three minutes (c = 3):
                                   

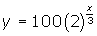
• the number of bacteria increases by a factor of 4 for every six minutes (c = 6):
                                  

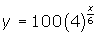
Example 1

A bacteria strain triples every 8 minutes. If there are 850 bacteria in the culture initially, write an equation to describe its growth. How many bacteria are in the culture after 12 minutes?

Solution

Using the equation  we have:

The initial value is 850, thus a = 850. Since we are talking about tripling, the common ratio is 3, thus  b = 3. This tripling or common ratio of 3 occurs every 8 minutes, thus c = 8. This gives the equation:

Substitute x = 12 into this equation to find the number present after 12 minutes

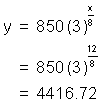
There are approximately 4417 bacteria in the culture after 12 minutes.

Example 2

The half-life of iodine is 4 days. If we start with a sample of 60 grams, how much remains after 22 days?

Solution

Using the equation we have:

The initial value is 60, thus a = 60. Since we are talking about half-life, the time at which half the quantity remains, the common ration is ½, thus b = ½.  The half life occurs every 4 days, thus c = 4 . This gives the equation:

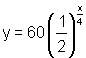
Substitute x = 22 into this equation to find the amount present after 22 days:

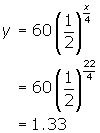
After 22 days 1.33 grams of the iodine remain.

Activity

1. If you have not already done so, complete Investigation 7 on page 134 in your text.
2. Complete the Investigation Questions 26 - 30 on pages 135 &136.
3. Do the CYU Questions 31 - 37, 39 on pages 136 - 138.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

Alcohol in the bloodstream is reduced by half every 3 hours. If there are in the bloodstream at the start of a test, how much remains after 8 hours.

Solution