Learning Resources

Investigation 6: Pennies from Heaven

Test yourself

Let 1975 be year 0. The other years then become year 5, 10, 15 , 20, etc. Enter this in List L1. Enter the corresponding populations in List L2. This is shown below:

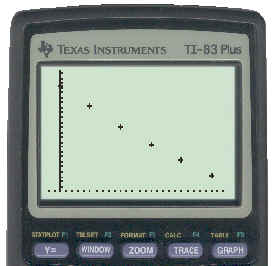
Now draw a scatter plot of this data that we have entered in Lists L1 and L2. This is shown below:

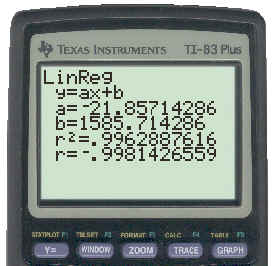
It is difficult to tell from the graph if it is linear or exponential. We will perform both a linear and an exponential regression and see which one "fits the best".

First the linear regression is shown below:

The r is referred to as a correlation coefficient and r2 as a coefficient of determination. They basically tell how good the regression equation fits the data. The closer they are to 1 the better the fit. Compare the values of these coefficients for the linear regression at the left and the exponential regression below. (Note: to get r and r2 displayed, you have to go to [CATALOGUE] and press [ENTER] at the DiagnosticOn command). Note the values of r and r2 for the exponential regression on the left. They are much closer to 1 than they were for the linear regression. The data in the table is thus more exponential than it is linear. The desired function that best models the data is thus: y = 1601 (0.9834)x

Next the exponential regression is completed:

To find what the population will be in 2005 if this trend continues, we substitute x = 30 (2005 is 30 years after the start of the data) into the regression equation. This gives:

y = 1601 (0.9834)³⁰ = 968.9

Since the population must be a whole number, we round the answer to 969.