
Learning Resources
Lesson
Investigation 3
In this part of the lesson you will explore the graph of y = bx for values of x less than zero and b greater than zero. Up to this point you have considered exponential functions of the form y = bx where x has been a whole number, viz. { 0, 1, 2, 3, 4, ... }.
You will look at the graph and, using the TI83, determine the value of y for a given value of x which is less than zero. You will concentrate first on the integer values for x which are less than zero, viz. {-1, -2, -3, -4, ... }.
For Step A, use your TI83 to draw the required graphs of the functions. Set x in the [WINDOW] between -4 and 4 and set y between -1 and the value that b4 will have for the particular value of b. Make sure to copy sketches of your graphs into your notebook for further analysis.
For Step B, the table for y = 2x is shown below.

If you want to see the keystrokes necessary to get this result click here.
To see the pattern suggested by the graph, the decimal representations of the y-values will have to be converted to fractional form. Recall for terminating decimals you have to use the place value to write a fraction and reduce to lowest terms. For example, to convert 0.75 to a decimal, write it as ![]() and reduce it to
and reduce it to ![]() .
.
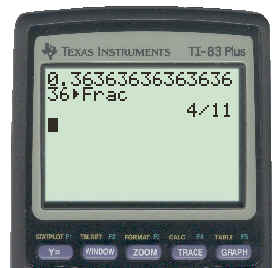
If the decimal is repeating, and you don't know its fractional equivalent, you can use the TI-83, to convert it to a fraction. Simply enter as many digits of the decimal as possible, select the [MATH] key to obtain its menu and select the first item 1:>Frac. Press [ENTER] and the fraction equivalent will appear. The screen below shows this done for 0.3636363636
Investigation Questions
For question 34 on page 119, the common point on the three graphs can be found from the graphs or from the table of values. This point common to all three is called the focal point . In fact, it is the point that all exponential functions of the form ![]() have in common.
have in common.
The results of the investigation and its questions should lead you to these facts:
- a zero exponent will give a y-value of 1 regardless of the base used.
- a base to a negative exponent can be evaluated by raising the base to the positive of the exponent and taking its reciprocal.
Now that we know it makes sense to use negative exponents, since they give points on the graph of the exponential functions, we want to look at a more formalized definition for them.
Focus C uses the laws for dividing exponents to justify and define the meaning of zero and negative exponents. Recall that for division of powers to the same base we simply subtract the exponents. For example:
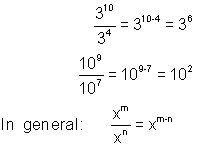
Applying this law to an expression where the exponent in the numerator is smaller than the exponent in the denominator leads to the definition of negative exponents. This is shown in the interactive below.
The definition of zero exponents can be shown using the same technique. You can read that in your text book.
Some examples of simplifying expressions that contain zero and negative exponents are given below.
1. ![]() 2.
2. 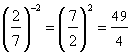
3. 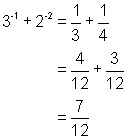 4.
4. 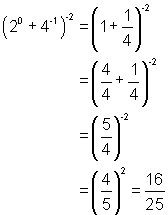
Activity
- Complete Investigation 3 on page 119 in your text.
- Complete the Investigation Questions 34 - 37 on pages 119 & 120.
- Read through the examples in Focus C on page 120.
- Complete the Focus Questions 38 - 40 on page 121.
- Do the CYU Questions 50 - 54 on page 123.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Simplify without negative exponents:
1. ![]() 2.
2. ![]()