Learning Resources

Lesson

For this lesson continue with the work on the Chapter Project started in the last section. The following hints and suggestions may help you to complete the project.

Part (h)
When x% of the circle is removed, the circumference of what remains forms the circumference of the base of the cone. This is (100 - x)% of the original circumference. For example, if 50% of the circle is removed, then so is 50% of the circumference:

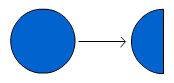
Justify the given expressions for each side of the triangle and then use the Pythagorean relationship to write h as a function in terms of x.

Part (i)
Recall  the volume of a cone is found by using the formula , where A represents the area of the base. The given expression can be found using this formula.

Part (j)
From Part (h), you should have . Replace this expression for h in the formula in part (i) . This will give the volume in terms of x. Use technology to graph the function.

Part (k)
Note that the Volume will be a maximum at the point where the slope of the tangent is zero. Interpret the changes in slope of the tangents in terms of increasing and decreasing volumes.

Activity

Complete the Chapter Project parts (h) - (k) on page 96 in your text.

Test Yourself

There are no test items for this lesson. However, be prepared to discuss the  project with your teacher and/or your fellow students.