Learning Resources

Lesson

A tangent to a curve at a point is a line that intersects a curve at a point and has the same slope as the curve at that point. The slope of a tangent can be approximated by taking the slope of a secant line which passes through the point of tangency and has its second point "very close" to the point of tangency. As the second point of the secant gets closer and closer to the point of tangency, the slope of the secant gets closer and closer to the the slope of the tangent. This is shown in the interactive below:

Instead of picking the tangent point as one of the points on the secant, we could have picked the points where the secant intersected the curve to be on either side of the tangent point. We would then move both secant points closer and closer to the tangent point to get a better and better approximation to the slope of the tangent.

Regardless of which points you choose, the method of finding the slope of a tangent to a curve at a given point is to approximate it by the slope of a secant passing through two points "very near" the tangent point.

In the last section we discovered that the average rate of change between two points on any curve was the same as the slope of the line passing through these two points and the line was called the secant. Since the tangent is the limiting position of the secant as the two points get closer and closer together, we can use it to define another type of change.

The instantaneous rate of change at a given point on a curve is the slope of the tangent to the graph at that point. There can be no gaps in the set of ordered pairs making up the graph which means the data has to be continuous.

Focus B in your text book shows an example of how these concepts can be applied. The first two steps in that example deal with setting up the equation which defines the relationship between the variables. Many times these two steps are not necessary because the defining equation is known or provided for you. That is the case in the example on the next page and in many of the examples in the assigned exercises in the text.

Example

Neglecting air resistance, the distance, d (in metres), an object falls when dropped from a height in time, t (in seconds), is given by the formula d = 4.9t².  If a marble is dropped from the top of the CN Tower, how fast is the marble traveling at 6 seconds?

Solution

The speed at 6 seconds is the instantaneous rate of change of distance in relation to time at 6 seconds, i.e. the speed. We thus require the slope of the tangent to the graph of the function at that point. So that we can "see" what we want, the TI83 was used to draw the graph and the tangent to it at t = 6. The results are shown below (more about how to do this later):

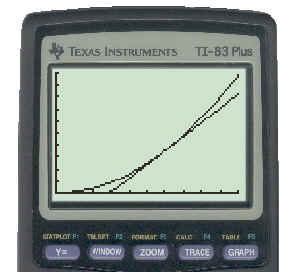
We will calculate the slope of a secant that has points on the graph of the function which are "very near" to the tangent point. Let's pick the values of t for the two points the secant passes through to be t = 6 and t = 6.01 (if we wanted a better approximation we could let t = 6.00001, or any value as close as we wish)

Now evaluate the function for these two values of t:

If t = 6, then d = 4.9 (6)² = 4.9 x 36 = 176.4

If t = 6.01, then d = 4.9 (6.01)² = 4.9 x 36.1201 = 176.988

Therefore, the two points on the graph that the secant passes through are:

(6 , 176.4)  and  (6.01 , 176.988)

We will use these two points to determine the slope of the secant, and that will be our approximation to the slope of the tangent at t = 6.

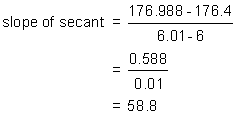
The slope of the tangent to the graph at t=6 is therefore approximately 58.8. This means that the speed of the marble at 6 seconds is approximately 58.8 m/s.

Verification

We can use the TI83 to verify our result. It will draw the graph of the tangent line to any curve at a specified domain value. It will then display the tangent and its equation. Since the coefficient of x in the linear equation y = mx + b is the slope, we can use it to check our result. Doing this for the equation in the example above, viz. y = 4.9x², we get the results indicated below:

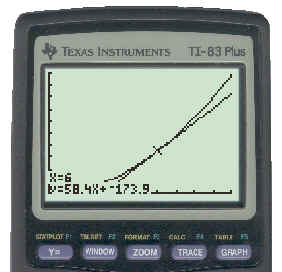
Note the equation of the tangent. It is y = 58.4x - 173.9. The slope is thus 58.4. We obtained 58.8 in our calculations in the example. How do you account for the difference? How could we make it less?

To see the key strokes necessary to do this on your TI83, click here.

Activity

1. Read through the example in Focus B on pages 87 - 89 in your text. 
   Step 1 and Step 2 define the function you are dealing with. In most of the exercises that follow, these steps are not necessary because the function is given to you. 
   Also, it is not necessary to do both Step 3 and Step 4. Decide on the accuracy you wish to achieve with your approximation and just do the calculation once.
2. Complete the Focus Questions 9 -13 on pages 89 & 90.
3. Do the CYU Questions 14 - 29 on pages 90 - 94.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

A water cooler cup is in the shape of a right circular cone. Water is being poured into it at a constant rate. The height of the water t seconds after it is started to be filled is given by the formula: 

Find the rate at which the water level in the cup is rising 0.5 sec after the start of the filling process.

Solution