Learning Resources

Lesson

The quadratic formula states that for the quadratic equation ax² + bx + c = 0, the solutions are given as:

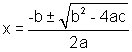
The part under the radical sign, b² - 4ac, tells a great deal about the roots of a quadratic equation. In fact, it is given a special name. It is called the discriminant and is usually represented with the letter D.

Discriminant = b² - 4ac

The purpose of this investigation is to discover the relationships between the discriminant, the roots of a quadratic equation, and the x-intercepts of the graph of the corresponding quadratic function.

If there is more than one student in your school doing this course, it is a good idea to share the work in this investigation and pool your results to discover the pattern. One person or group could use the set of equations in Step A, a second person or group could use the equations in Step D part (i), and a third person or group could use the equations in Step D part (ii).

For Investigation 6 on page 55 of your text, it is a good idea to use a table like the one below to record your results for Steps A, B and C. Then repeat the table for the equations in Step D parts (i) and (ii). By the "type of roots" we mean if they are real or complex. Recall that discussion from the work on the quadratic formula.

General Form
Transformational Form
Vertex
Number of x-intercepts
Discriminant
Types of Roots

Notes on Investigation 6

Step A

The first equation has been put in transformational form for you as a reminder of how to do the process:

 

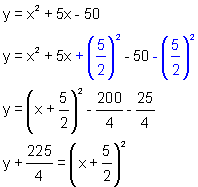
The vertex is thus at   

Step B

Since the vertex is at   and the parabola opens upward, the graph should cut the x-axis (i.e. have x-intercepts) at two points. 

To confirm this, draw the graph of the function using the TI83 as shown below. Alternately, you can use the transformational form of the equation and sketch its graph by translating the graph of y = x² to the left  2.5 units and down 56.25 units. There is no vertical stretch.

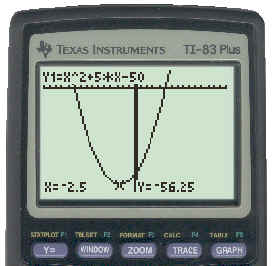
Step C

Use the a, b and c from each function to calculate the value of , the discriminant.

Make note of whether the discriminant is positive, negative or zero. Compare this to the number of roots of the equation and the number of x-intercepts (zeros) of the corresponding function.

What is the relation between the discriminant and (i) the number of roots of the equation ax² +bx + c = 0 and (ii) the number of zeros (x-intercepts of the function y = ax² +bx + c = 0?

Before you continue, stop and complete Investigation 6 on page 55 in your text book.

You should have discovered from the investigation and its questions that the discriminant tells you a number of facts about the roots of a quadratic equation, and about the zeros and x-intercepts of the graph of the corresponding quadratic function. You should have discovered: 

• If b² - 4ac > 0, the graph of the function will have two x-intercepts, and the equation will have two unequal real roots.
• If b² - 4ac = 0, the graph of the function will have one x-intercept, and the equation will have two equal real roots. It is sometimes also said that the this type of equation has a double root.
• If b² - 4ac < 0, the graph will have no x-intercepts, and the equation will have two roots are not real but complex.

Activity

1. If you have not already done so, complete Investigation 6 on page 55 in your text. See the notes in the lesson for some help on how to proceed with this investigation.
2. Complete Investigation Questions 51 - 55 on pages 55 & 56.
3. Do the CYU Questions 56 - 61 on pages 56 & 57.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

• Without solving, decide if the following equations have (a) two unequal real roots, (b) two equal real roots (a double root), (c) no real roots.

1. 2x² -12x + 18 =0

2. 2x² -12x + 19 =0

3. 2x² -12x + 15 =0

Solution