Learning Resources

Lesson

Consider the general quadratic equation ax² + bx + c = 0. If we were to apply the technique of completing the square to solve this equation we would get:

 

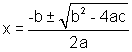
This result is known as the quadratic formula. Although you are not responsible for its derivation, if you would like to see how to derive it by completing the square, click here.

If a quadratic equation is written in the general form, the values of a, b, and c can be read directly from it and substituted into this formula. It is then a matter of working out the expression to find the solution. This is shown in the example below.

It is possible for the expression under the radical sign to evaluate to a negative number.

In your earlier work with radicals, you learned that the square root of negative numbers does not exist in the real number system. For example, we have no real number that is . It simply does not exist in the real number system.

However, such numbers occur frequently in mathematics when we attempt to solve equations like:

x²  =  -1

In response to this problem, another system of numbers is used. It is called the imaginary number system. In this system we define to be the number i . Some examples of how it can be used are shown below:

                                 
                                 
                                 

The imaginary numbers and the real numbers can be combined into a set called the complex numbers. These numbers have a real part and an imaginary part and are usually written as a + bi. The example in the interactive below shows how these numbers occur in solving quadratic equations.

As a note, mathematicians first referred to these types of numbers as imaginary numbers because they seemed not to exist. However, imaginary numbers do exist and have many applications in the sciences, notably in the area of electronics. Despite their name, they are not really imaginary at all. The name dates back to when they were first introduced, before their existence was really understood. At that time, people were imagining what it would be like to have a number system that contained square roots of negative numbers, hence the name "imaginary".

1. The roots of the quadratic equation ax² + bx + c = 0 and the zeros of the quadratic function y = ax² + bx + c are the same thing.
   
2. The roots of the quadratic equation ax² + bx + c = 0 can be found by:
   (a) graphing y = ax² + bx + c and reading the x-intercepts.
   (b) factoring
   (c) completing the square
   (d) the quadratic formula
   
3. It is possible that the roots of a quadratic equation are not real numbers. The number system used to answer these problems is the complex number system. A complex number is of the form a + bi where i = .
   
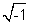4. If a quadratic equation has complex roots, then it follows that the graph of the corresponding quadratic function has no x-intercepts.

Activity

1. Read through Investigation 5 on pages 47 & 48 in your text. If you find you need some help in completing this  investigation, click here.
2. Complete investigation questions 23 - 29 on pages 48 & 49.
3. Do the CYU Questions 30 - 32 on page 49.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

After you do the assigned activities, click on the Test Yourself button at the top of the page for a quick quiz on this  lesson.

Test Yourself

Solve the following equation  : 

Solution