Learning Resources

Lesson

Before we begin work on the outcomes of this lesson, let's review the three forms of the quadratic function and what each form tells us about the graph.

General Form 

The general form is y = ax² + bx + c.

The value of a, the coefficient of x² , tells the direction of opening (up if positive and down if negative) and the vertical stretch. The value of c, the constant term tells the y-intercept. The coordinates of the point where the graph cuts the y-axis is thus (0 , c).

For example, the graph of the equation y = 2x² + 3x - 4 is a vertical stretch of 2 of the graph of y = x² . It opens upward and the y-intercept of the graph is -4.

Standard Form

The standard form is y = a(x - h)² + k. 

The value of a again tells the direction of opening and the vertical stretch. The coordinates of the vertex of the parabola are (h , k) and the axis of symmetry is given by the equation x = h.

For example, the graph of the equation y = 3(x + 2)² - 5 is a vertical stretch of 3 of the graph of y = x² . The vertex of the parabola is at (-2 , -5),  the equation of the axis of symmetry is x = -2, and the curve opens upward.

Transformational form

The transformational form is . The value of a again tells the direction of opening and the vertical stretch. The coordinates of the vertex of the parabola are (h , k) and the axis of symmetry is x = h.

For example, the graph of the equation -4(y - 2) = (x + 3)² is a vertical "stretch" of ¼ of the graph of y = x² . The vertex of the parabola is at (2 , -3),  the equation of the axis of symmetry is x = -3 and the curve opens downward.

The transformational form and the standard form are very similar and it is easy to change one form into the other as we did in the last lesson. This is shown below to emphasize the similarity between them.

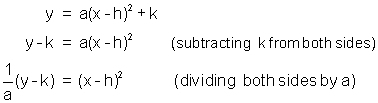
To get the general form was a matter of expanding the binomial in the standard form and simplifying.

What we now wish to do is change the equation of a parabola from general form to transformational form (or standard form since the two are so similar to each other).

To begin, let's look at the expansion of some binomials to see if we can discover a pattern that may be helpful later on.

We will now apply the pattern that you discovered above to help change the equation of a parabola from general form to standard and then to transformational form.

Example 1

Write y = x² + 8x - 3 in standard and transformational form.

Solution

From the transformational form of the equation in this example we can determine the following:

• The curve opens upward and there is no vertical stretch.
• The coordinates of the vertex are (-4 , -19).
• Because the curve opens upward, the vertex is the lowest point . Therefore the minimum value of the function is -19 and the value of x that gives this minimum is -4.
• The equation of the axis of symmetry is x = -4

The previous example dealt with an equation where the coefficient of the squared term was one. We now want to look an example where the coefficient is some number other than 1.

Example 2

Write y = 2x² - 10x + 6  in standard and transformational form.

Solution

From the transformational form of the equation in this example we can determine the following:

• The curve opens upward and the vertical stretch is 2.
• The coordinates of the vertex are (6 , -66).
• Because the curve opens upward, the vertex is the lowest point . Therefore the minimum value of the function is -66 and the value of x that gives this minimum is 6.
• The equation of the axis of symmetry is x = 6

The final example deals with a function that has a negative fraction for the coefficient of the squared term. The procedure is the same but you have to be careful with the numbers.

Example 3

Write y = -¼ x² + 2x - 3 in transformational form.

Solution

From the transformational form of the equation in this example we can determine the following:

• The curve opens downward and the vertical stretch is -¼.
• The coordinates of the vertex are (4 , 1).
• Because the curve opens downward, the vertex is the highest point . Therefore the maximum value of the function is 1 and the value of x that gives this maximum is 4.
• The equation of the axis of symmetry is x = 4

The procedure used in this lesson for rearranging a quadratic from the general to the transformational form is different that the one in your text. Read through what is in the text and use the method you find the easiest.

Activity

1. Read through Example 4 in Focus D on pages 31 & 32 in your text. It is an alternate to the method presented in the lesson.
2. Complete Focus Questions 14 (if you choose the text method), 15 - 22 on pages 32 & 33.
3. Do CYU Questions 23 - 30 on pages 34 & 35.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

After you do the assigned activities, click on the Test Yourself button at the top of the page for a quick quiz on this  lesson.

Test Yourself

1. Write the quadratic y = -2x² + 6x + 11 in transformational form. Give its maximum or minimum value.
2. The hammer throw is a very competitive event in the Summer Olympics. If  the height in metres, h, reached by the hammer after t seconds of flight for one of the competitors is given by the formula h = -5t² + 20t +1.5, what is the maximum height reached by the hammer?

Solution