Learning Resources

Lesson

To maintain the central theme of the unit, a chapter project is included for each unit in this textbook. The project is introduced early and builds as you attain the necessary skills and knowledge. It is usually completed as the chapter ends and models the processes used to solve real world problems. 

This is the same type of project used in Mathematics 1204 and 2204. As each part is introduced it should be completed in its entirety. That way, if you are requested, you can submit it to your on-line teacher, either at the end of the unit or at any time throughout  the unit, for evaluation purposes.

To effectively manage a chapter project you should

• set up a chapter project folder or binder
• copy the essential information from each part of the project into your folder
• include diagrams, models, pictures or any other support material
• date and complete each stage of the project
• write any impressions or comments concerning the project at the end of each entry

This project will continue to build in sections 1.2, 1.3 and 1.4. Complete each stage as it is presented. 

Good luck with the start of your first project!

For this problem, the 100 meters of fencing has to be used to enclose two separate square plots. For example, if 8 metres is used for one plot then 92 metres must be used for the other plot.  In general, if x metres is used for the perimeter of one plot, then 100 - x is used for the perimeter of the other.

Of course these lengths will be the perimeter of each plot. Since these are square plots, each side will be one quarter of the perimeter which means in the above example the sides are 2 and 13 respectively. This is shown below

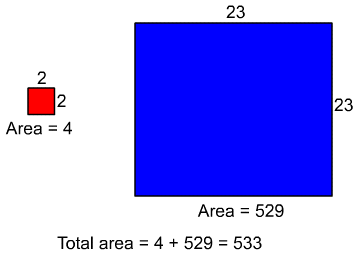
For question (a), set up a table like the one below and record the perimeter of one in the top row and the total area of both in the bottom. The above example has been filled in for you. 

Perimeter of one square	1	2	3	4	5	6	7	8	9	10
Total area of both								533

For question (b), you should show by calculating the sequence of differences, that the above sequence can be represented by a quadratic of the form:
                                               y = ax² + bx + c

It is then a matter of finding the value of a , b, and c to suit the data in the table. If you have done Question 23(c) on page 9 you will have discovered that the common difference is twice the value of a, the coefficient of x². Use the common difference you found for this sequence (it should be D₂ = 0.25 if you have done your calculations correctly) to write the quadratic with this in place of a.

To find b and c, substitute in any two ordered pairs from the table (e.g. (8 , 533) , (1 , ?) , (2 , ?), etc.) and set up a system of equations in b and c. Solve this system by one of the methods you learned in Mathematics 2204 (Section 1.3 on page 25 of Mathematical Modeling, Book 2).

Activity

• Complete parts (a) & (b) of the Chapter Project on page 14 in your text.

Test Yourself

There are no extra questions for this lesson. Simply submit your work to date to your online teacher.