Learning Resources

Lesson

In this lesson we will look at sequences that are not arithmetic. To do this we will first explore the example presented in Investigation 2 on page 7 of your text. However, to generate the sequence we will use the reasoning presented in Ex. 17 on page 8.

Step A & B

Step C & D

To determine if the sequence you generated in Step A  is arithmetic, find the sequence of differences.

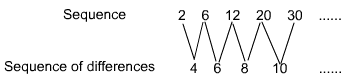
Note that the sequence of differences does not give a common difference. Therefore the sequence is not arithmetic.

The sequence of differences found above is referred to as the sequence of first-level differences and it is usually represented as D₁. Let's consider this first-level sequence of differences and use it to find another sequence of differences as shown below:

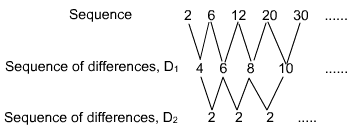
The last sequence is referred to as the sequence of second-level differences and, as indicated, is usually denoted as D₂. Note that this sequence does give a common difference.

We learned in the previous lesson that an arithmetic sequence has a common difference at the first level and the graph of the term number verses the term value gave a straight line and the function which defined it was linear.

We now wish to look at the graph of sequences whose second level differences are constant and determine the type of function which generates such a sequence.

To construct the graph we will set up a table relating the number of outlets to the number of options for buying two lunches and then plot the points on a grid.

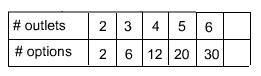
Plotting these points on a graph gives:

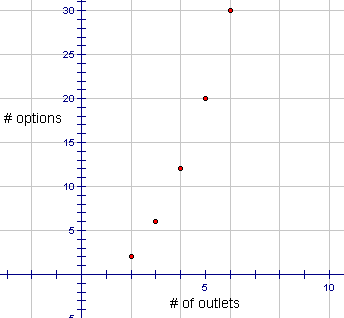
Clearly the above graph is not linear. If we extend the domain to include all real numbers instead of just the positive integers the shape of the graph and the function rule involved should look familiar to you.

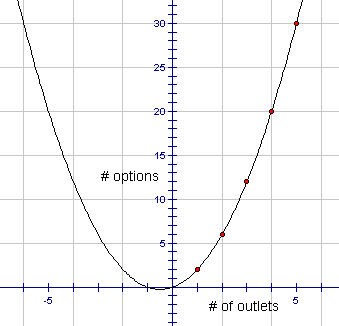
From your work in Math 1204, you should recognize the above graph as the graph of quadratic or second degree function.

In the above example, if the number of outlets is represented by n, then the number of choices for Alice is n and for Beatrice the number of choices is
n - 1. The total number of options is thus given by the rule or formula:

# options = n(n - 1) = n² - n

Test this rule for generating the values in the table above. For example, for 3 outlets,

# options = n² - n = 3² - 3 = 6

It looks as though quadratic functions can generate sequences where the second level differences are common. In the work assigned in your text book you will explore this further and note the relation between the level at which the common difference occurs and the power of the function which generates its terms.

The terms of a sequences like the one above can be generated from the defining function using the TI83. Also, you can use the TI83 to generate the sequence of differences for a given sequence. The keystrokes necessary for both of these can be seen by clicking here >>.

Now go to the top of the page and click on the Activities button.

Activity

1. Complete Investigation 2 on page 7 in your text.
2. Complete Investigation Questions 17 to 21(a) on pages 8 & 9.
3. Do CYU Questions 22, 23 (a) - (c), 26, 27 (a)& (b), 29  - 32 on pages 9 - 11.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

After you do the assigned activities, click on the Test Yourself button at the top of the page for a quick quiz on this  lesson.

Test Yourself

Use each function below to generate 10 terms of the sequence. For each, find the sequence of differences until you obtain a common difference. What do you notice?

1. t_n = 2n - 3
   
2. t_n = 2n² - n + 3
   
3. t_n = 2n³ - 7n

Solution