Centre for Distance Learning and Innovation

Home » » Courses » Mathematics » Mathematics 3103 (delisted) » Unit 05 » Set 01 ILO 04 » Go to Work

Lesson

Before we investigate the inverse of a quadratic function, let us review the quadratic function itself and its graph.

A quadratic function is one that can be written in the form f(x) = a(x - h)² + k. It is a transformation of the basic quadratic q(x) = x² , whose graph is a parabola.

The parabola f(x) = a(x - h)² + k has vertex (h , k), and axis of symmetry x = h. This information is critical in understanding the restrictions necessary so that the inverse will be a function.

First we will look at the quadratic itself.

Example 1

Graph the parabola p(x) =

Solution

Axis of symmetry, x = -2 ; the vertex (-2 , -3) ; one other point on the graph (found by substituting x = 2 into the equation) is (2 , 1).

We now wish to consider the inverse of the above function in a little more detail than we did in Lesson 02 of this Unit. That is done on Page b of this lesson.

We learned in Lesson 02 how to draw the graph of the inverse of any given graph by reflecting it in the line y = x. Let us apply this technique to the graph of
Example 1 on Page a of this lesson.

Example 1

Graph the inverse of p(x) =

Solution

The details of finding the points in the reflection of line y = x are left to you (if you forget how to do this, refer to Example 2 on page b of Lesson 02 of this Section). The graph of the function p and its inverse are shown below. Note the mirror image, i.e. reflection in the line y = x.

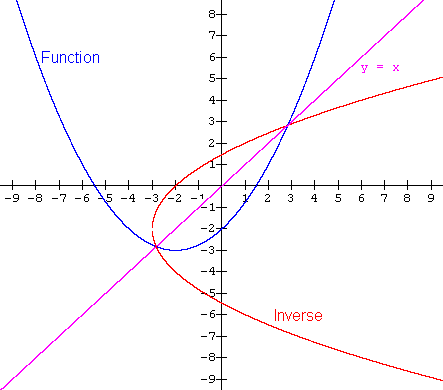
Clearly the inverse is NOT a function, because for a given value of x there are two values for y. For example, when x = 6 , y = 4 or -8.

However, if we restrict the graph of function p to just that part to the right of the axis of symmetry (i.e. restrict the domain of p to x ³ -2) and find the reflection of it in the line y = x we get.

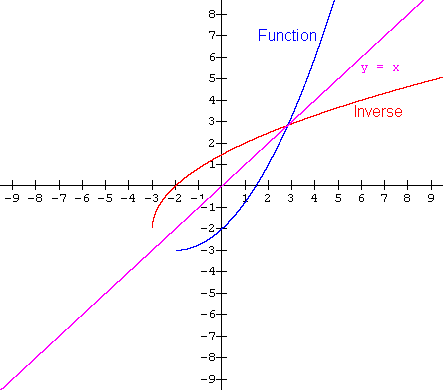
Note that if we use the horizontal line test on the graph of the function p (the blue graph), it never cuts it in more than one point. We thus expect its inverse to be a function.

Looking at the graph of the inverse (the red graph) we see that it is indeed a function because no two ordered pairs contain the same first coordinate (apply the vertical line test for functions).

We could also restrict the domain of the function p to x £ -2 (i.e. the part to the left of the axis of symmetry). That would give the following result.

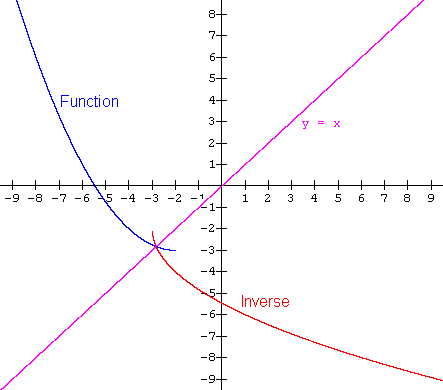
Again we see that the inverse is a function, as we would expect if we had applied the horizontal line test to the restricted graph of function p.

From the above example, you should be able to see the following:

The inverse of the quadratic function f(x) = a(x - h)² + k is not a function.
We can make the inverse of f(x) = a(x - h)² + k a function by restricting the domain of f to x ³ h or to x £ h.

We now wish to turn our attention to finding the algebraic form of the inverse of any given quadratic.

The technique for finding the inverse of a given quadratic function is the same as finding the inverse of a linear function. We simply write the function in the "y =" form, interchange the x and y variables, and solve the resulting equation for y. This is shown in the following examples.

Example 1

Find the inverse of f(x) =

Solution

First write the function in "y =" form: y =

Then interchange the x and y variables: x =

Solve the resulting equation for y: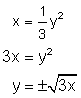

Thus the inverse is

Note the in the above equation for the inverse. We saw the necessity of that earlier in this course when we were solving quadratics. For example, recall that if
x² = 4, then x is 2.

Also note that because there are two values of y ( a positive and a negative) for each value of x (except when x = 0), the inverse is not a function. We will discuss on Page d of this lesson what the inverse will be if we restrict the domain of f as suggested on Page b of this lesson.

Example 2

Find the inverse of g(x) = -2(x + 1)² -3

Solution

First write the function in "y =" form: y = -2(x + 1)² -3

Then interchange the x and y variables: x = -2(y + 1)² -3

Solve the resulting equation for y: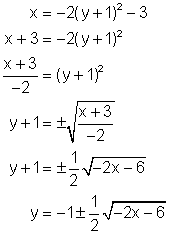

Again the inverse is not a function. There are two values of y for each value of x. They are and .

Sometimes the quadratic is not in the form y = a(x - h)² + k. In that case we need to rearrange it and put it in that form before we start to solve. This is shown in the following example.

Example 3

Find the inverse of h(x) = 2x² - 16x + 32

Solution:

First write in y = a(x - h)² + k form: y = 2x² - 16x + 32

y = 2(x²-8x+16)

y = 2(x - 4)²

Interchange the x and y variables: x = 2(y - 4)²

Solve the resulting equation for y: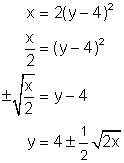

Again the inverse is not a function. There are two values of y for each value of x. They are and

Still another step that may have to be taken before we can find the inverse is to apply the technique of completing the square before we start to solve. If you have already covered this technique in earlier courses you should have no problem. If you do not know how to complete the square on a quadratic polynomial, study the following example and if necessary contact your teacher for extra help.

Example 4

Find the inverse of f(x) = x² + 6x + 3

Solution

First write in y = a(x - h)² + k form: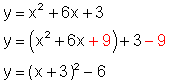

Interchange the x and y variables: x = (y + 3)² - 6

Solve the resulting equation for y: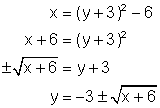

Again the inverse is not a function. There are two values of y for each value of x. They are and

We now want to turn our attention to restricting the domain of the original function so that the resulting inverse is also a function.

Let us start by reconsidering the quadratic function in Example 2 on the previous page.

The function g(x) = -2(x + 1)² -3 has axis of symmetry x = -1, vertex (-1 , -3) opens downward and contains the point (0 , -5). Its graph looks like:

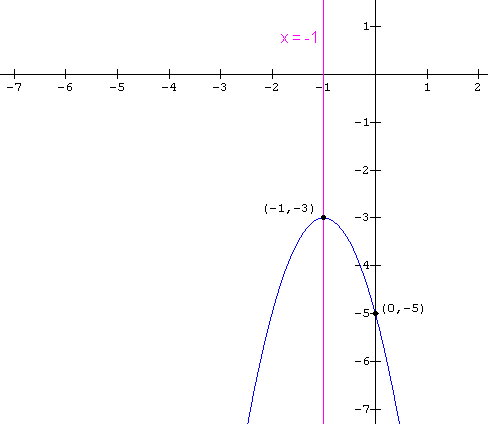
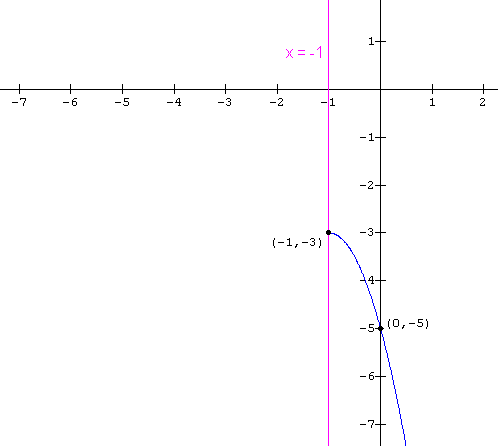
As noted in Example 2 on the previous page, the inverse of this function is not a function. But now restrict the domain to points to the right of the axis of symmetry. In other words, consider the function:

f(x) = -2(x + 1)² -3 with Domain = {x | x ³ -1}

Its graph looks like:

And the graph of its inverse looks like:

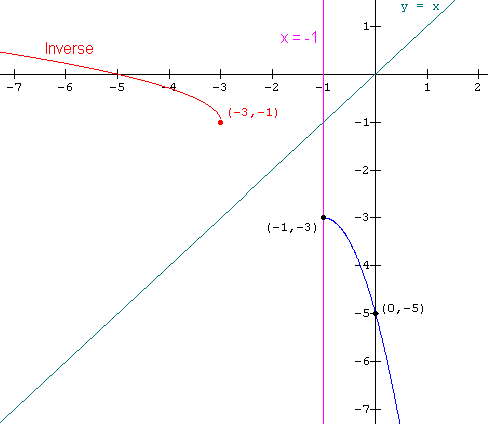
This inverse is a function and we can therefore write the equation for it using the notation. But what is its equation?

Recall the answer to Example 2 on the previous page that the inverse of
g(x) = -2(x + 1)² -3 was ,which we said gave two values for y for each value of x, viz. and . So one of these expressions is the inverse for the function to the right of the axis of symmetry and the other is for the function to the left of the axis of symmetry.

To check whether to use the + or the - radical part for the inverse we have considered, we can substitute in a value and check.

For example, if x = -5, then:

Clearly from the graph it is the positive radical part we want because (-5 , 0) is on the inverse graph, but (-5 , -2) is not.

Thus: f(x) = -2(x + 1)² -3 with Domain = {x | x ³ -1},

has inverse:

Without going into further details, you should be able to conclude that:

f(x) = -2(x + 1)² -3 with Domain = {x | x £ -1},

has inverse:

Note: Generally the positive radical part gives the inverse of the function restricted to the right of the axis of symmetry and the negative radical part gives the inverse restricted to the left of the axis of symmetry.

Example 1

Find (x) , given that f(x) = with domain = {x | x £ 1}

Solution

Ignore the domain restriction and proceed as before:

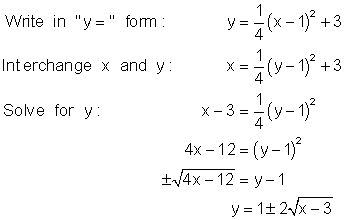
Now apply the domain restriction which limits the function f to points to the left of the axis of symmetry x = 1. The inverse of this restricted function is a function and is defined by the negative part of the radical. Thus:

Example 2

Find (x) , given that f(x) = x² - 8x + 1 with domain = {x | x ³ 4}

Solution

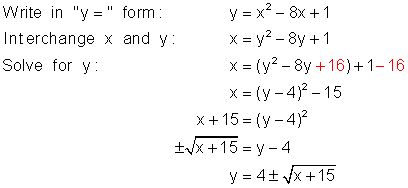
Now apply the domain restriction which limits the function f to points to the right of the axis of symmetry x = 4. The inverse of this restricted function is a function and is defined by the positive part of the radical. Thus:

Activity

For the functions in the exercises below: (a) find the inverse, (b) give a restriction of the domain of the original function that would make the inverse a function and then write the inverse for this restricted function using inverse function notation.