Learning Resources
Lesson
In the Lesson 02 in this Section you were given two functions and asked to determine if they were inverses of each other. But what if you are only given one function and asked to determine the equation of its inverse and whether that inverse is a function? That is what this lesson will discuss for the case when the given function is linear.
To find the equation of the inverse, we will rely on an important point we learned in the previous lesson about inverses. It stated:
"If two functions are inverses of each other, the range values of one become the domain values of the other. If we think of a function, f , as a set of ordered pairs (x , y), then its inverse function, g , is the set of ordered pairs (y , x). That is, we simply interchange the x and y coordinates of both functions.
To see how this works, look at the following examples.
Example 1
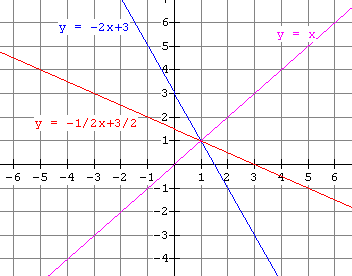
Find the inverse of f(x) = -2x + 3 . Then sketch f and its inverse on the same set of axes showing also the line of reflection.
Solution
Since the points that satisfy the function take the form (x , y), we can write the function as:
y = -2x + 3
The points that satisfy the inverse take the form (y , x), thus we can interchange the x and y in the original function and write the inverse as:
x = -2y + 3
Now solve this equation for y: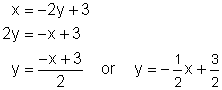 
Clearly this is a linear function whose graph has slope 
and y-intercept 
. We therefore can write this inverse in functional notation.
We do not want to use g , or some other letter, to represent this inverse function. We want to connect it to the original function f. The notation that is commonly used to represent the inverse of function f, when that inverse is a function, is 
. Thus we can write the inverse of f(x) = -2x + 3 using functional notation as:
CAUTION: Do not confuse this notation for the inverse function, 
, with the negative exponent notation used for real numbers and the variables that represent them. Recall that if x represents a real number, then x-1 means 
, which is the reciprocal or multiplicative inverse of x. If we wish to write the reciprocal of the range values of f(x) we must write 
or 
, which is not the same as the value of (x).
The graphs are:
Example 2
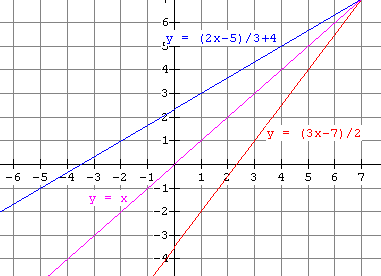
Find 
given that g(x) = 
and sketch both on the same set of axes.
Solution
Since the points that satisfy the function take the form (x , y), we can write the function as:
The points that satisfy the inverse take the form (y , x), thus we can interchange the x and y in the original function and write the inverse as:
Now solve this equation for y:
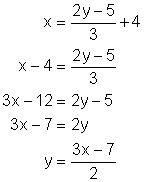
Thus we have: 
or 
which is a line with slope 
and y-intercept 
and is therefore a function.
The graphs are:
Example 3
Show that the inverse of any linear function is also a linear function.
Solution
You know that any linear equation can be represented in the form y = mx + b and is a function whose graph is a straight line with slope m and y-intercept b.
By finding the inverse of the function in this form, we will show that all linear functions have inverses that are functions.
Interchange x and y in the equation y = mx + b to get:
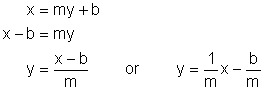
Provided m ¹ 0 , this is the equation of a line with slope 
and y-intercept 
and is thus a function. We can thus say that if g(x) = mx + b then 
.
If m = 0 in the above equation, the initial function is the constant function and its graph is a straight line. The graph of its inverse is a vertical line and is not a function (see Example 1(e) in the Pre-Test).
Activity
For each of the following functions, (a) find its inverse and, when it is a function, write it using the inverse function notation, (b) sketch the graph of the function and its inverse on the same set of axes.
1. f(x) = 3x
2. g(x) = -x + 3 (Before you check the answer for this problem, find the inverses of p(x) = -x ; r(x) = -x - 2; w(x) = -x + 1.5 . What do you notice about the graphs of the inverses of these functions? Why is this so?)
3. h(x) = 0.8(x - 2.3) + 3.2
4. 
5. p(x) = - 3
6. 
Test Yourself
For each of the following functions, (a) find its inverse and, when it is a function, write it using the inverse function notation, (b) sketch the graph of the function and its inverse on the same set of axes.
1. 
2. 