
Learning Resources
Inverse Functions Defined |
Answers to pre-test |
| 1(a) They are inverse functions because applying
one
after the other (composing
them) to any given
value, x , in the domain
returns the value, x , you
started with.
( ( |
1(b) 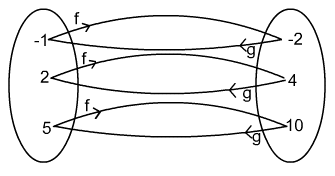 |
| 2(a) They are not inverse functions because
applying one
after the other (composing
them) to certain values
in the domain returns a
different value than what
you started with.
( ( Thus if x is
negative, ( |
2(b) 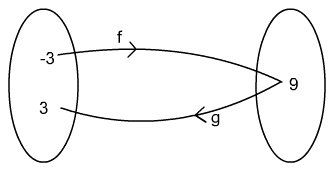 |
3(a) 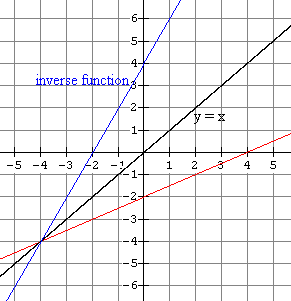 |
3(b) 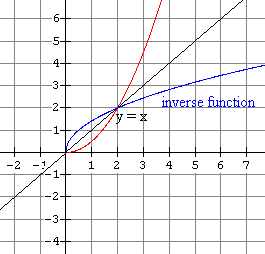 |
3(c)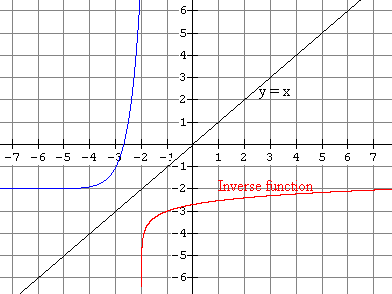 |
4(a) 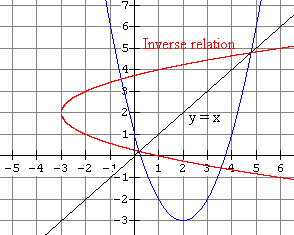 |
| 4(b) The inverse is not a function because for a particular value of x there are two values for y. For example when x = 1 we have y = 0 and 4. Also, the vertical line test applied to the inverse graph shows that it is not a function. |
| 4(c) To determine if a function has an inverse
that is a
function, we can use a
horizontal line test. If a
horizontal line cuts a graph at
two or more points, the inverse of its function is not a function, or we may say it has no inverse. |