
Learning Resources
Lesson
The composition of functions is a way of combining two or more functions to get a new function.
For example, suppose that y = f(x) = ![]() and that x = g(u) = u2 + 1. Since y is a function of x and x is, in turn, a function of u, it follows that y is ultimately a function of u. We can compute this function of u for y by substituting as follows:
and that x = g(u) = u2 + 1. Since y is a function of x and x is, in turn, a function of u, it follows that y is ultimately a function of u. We can compute this function of u for y by substituting as follows:
y=f(x) = f(g(u)) =f(u2 +1) = ![]()
The procedure is called composition because the new function is composed of the two given functions f and g.
In general, given any two functions f and g, we start with a number x in the domain of g and find its image g(x). If this number g(x) is in the domain of f, then we calculate the value of f(g(x). The result is a new function h(x) = f(g(x) obtained by substituting g into f. It is called the composition (or composite) of f and g and is denoted by ![]() (read as "f circle g").
(read as "f circle g").
Definition Given two functions f and g, the composite function ![]() is defined
is defined
by:
(![]() )(x) = f(g(x))
)(x) = f(g(x))
The domain of ![]() is the set of all x values in the domain of g such that g(x) is in the domain of f. In other words, (
is the set of all x values in the domain of g such that g(x) is in the domain of f. In other words, (![]() )(x) is defined whenever both g(x) and f(g(x)) are defined.
)(x) is defined whenever both g(x) and f(g(x)) are defined.
One way of picturing the composition of functions f and g, ![]() , is to use the "function machine" from earlier grades.
, is to use the "function machine" from earlier grades.
Press [show] to see how composition of functions can be modeled using a "function machine".
We can further see how this function machine analogy works by taking two particular functions. For example, if f(x) = x2 and g(x) = 3x + 1, then (![]() )(-1) can be modeled as follows:
)(-1) can be modeled as follows:
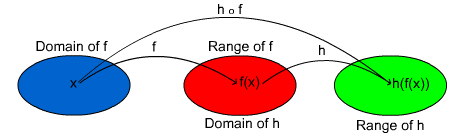
Another way to picture composition of functions is to use a mapping diagram.
The mapping diagram shows not only the relation between f , h , and ![]() , but also the relation between the domain and range of these functions.
, but also the relation between the domain and range of these functions.
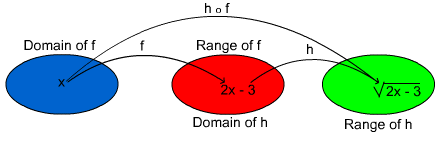
We can further see how this mapping diagram works if we consider two particular functions. For example, if f(x) = 2x - 3 and h(x) = ![]() , then
, then ![]() is shown as:
is shown as:
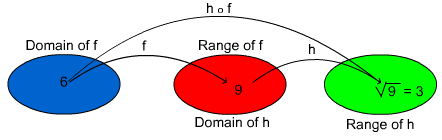
We can also use this method to evaluate ![]() for particular values of the domain. For example find (
for particular values of the domain. For example find (![]() )(6) and (
)(6) and (![]() )(1)
)(1)
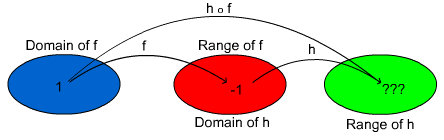
Note the last diagram above. We are not able to find (![]() )(1) because we are looking for the square root of a negative number and that is not a real number. This highlights the point in the definition on Page a that the domain of
)(1) because we are looking for the square root of a negative number and that is not a real number. This highlights the point in the definition on Page a that the domain of ![]() are those values of the domain of f for which h is defined.
are those values of the domain of f for which h is defined.
Look at the above functions again. For ![]() to be defined, we must restrict the domain of f so that its range values (which become the domain values of h) are not negative. That is,
to be defined, we must restrict the domain of f so that its range values (which become the domain values of h) are not negative. That is,
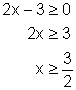
Thus the domain of (![]() )(x) is
)(x) is ![]()
Consider the following additional example. Suppose f(x) = ![]() and g(x) = 3x-6. Then the composite function (
and g(x) = 3x-6. Then the composite function (![]() )(x) = f(g(x)), and the range of g cannot contain zero, since zero must be excluded from the domain of f. We thus restrict the domain of g so that it does not give a range value of zero. That is:
)(x) = f(g(x)), and the range of g cannot contain zero, since zero must be excluded from the domain of f. We thus restrict the domain of g so that it does not give a range value of zero. That is:
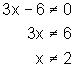
Thus the domain of ![]() is all real numbers except 2. We can state this as:
is all real numbers except 2. We can state this as:
Domain ![]() = {x | x ¹ 2}
= {x | x ¹ 2}
Although the domain and range of composite functions are optional topics in this course, you should be aware that the it is a very important concept and one that you will no doubt encounter in your future study of mathematics. Therefore a discussion of it is included in this lesson, however your teacher may decide not to require you to do the work related to it.
From the work on the preceding pages, it should be obvious that we can compute the value of (![]() )(x) and (
)(x) and (![]() )(x) for any particular value of x by simply applying the functions in turn. So why compute a general function, say F(x) for (
)(x) for any particular value of x by simply applying the functions in turn. So why compute a general function, say F(x) for (![]() )(x)?
)(x)?
The answer to that question will become apparent as you continue with your study of mathematics, in particular with the study of differential calculus. In order to differentiate many functions you have to use something called the Chain Rule. It relies on decomposing the function into its component functions.
Thus , for example, to differentiate F(x) = ![]() we might let y =f(u) =
we might let y =f(u) = ![]() and let u = x2 + 1. Then we can write y = F(x) = f(g(x)) = (
and let u = x2 + 1. Then we can write y = F(x) = f(g(x)) = (![]() )(x) and the Chain Rule tells us how to differentiate this.
)(x) and the Chain Rule tells us how to differentiate this.
However, before we can find the decomposition of functions we need to know how to find their composition. That is what we will concentrate on in this course. The examples in the Activities section will provide the background skills for this later work.
If that does not convince you for the need to study composition of functions, simply think of it as a means of shortening calculations. Imagine you had to set up a table of ten values for f(g(x) in Example 1 below. It is much more efficient to find the composite function first and then find the ten values by substituting directly into it, rather than find ten values for g(x) and substitute these ten values into f(x).
Below are some examples to help you understand the process of finding the composition of two functions.
Example 1
If f(x) = 4x + 5 and g(x) = 2x - 1, find (i) (![]() )(x) ; (ii) (
)(x) ; (ii) (![]() )(x) . What is the domain of each composite function?
)(x) . What is the domain of each composite function?
Solution (i)
Since the composite function is linear, and both of the original functions are linear, we can state:
Domain of ![]() = {All real numbers}
= {All real numbers}
Solution (ii)
Since the composite function is linear, and both of the original functions are linear, we can state:
Domain of ![]() = {All real numbers}
= {All real numbers}
Example 2
If f(x) = 2x2 - 3 and g(x) = 4x + 1, find (i) (![]() )(x) ; (ii) (
)(x) ; (ii) (![]() )(x). What is the domain of each composite function?
)(x). What is the domain of each composite function?
Solution (i)
The composite function is quadratic and we know that the domain of a quadratic function is the set of all real numbers. Also, the original functions have no restrictions on their domains. Thus we can state:
Domain of ![]() = {All real numbers}
= {All real numbers}
Solution (ii)
The composite function is quadratic and we know that the domain of a quadratic function is the set of all real numbers. Also, the original functions have no restrictions on their domains. Thus we can state:
Domain of ![]() = {All real numbers}
= {All real numbers}
Note: If the domain of the composite function is not specified it is generally
understood to be the set of all real numbers. Thus in the above examples
we could have omitted specifying the domain.
The solutions to the remaining examples are presented in static form, as you should now have the concept of the procedure to follow.
Example 3
If f(x) = ![]() and g(x) =
and g(x) = ![]() , find (i) (
, find (i) (![]() )(x) ; (ii) (
)(x) ; (ii) (![]() )(x). What is the domain of each composite function?
)(x). What is the domain of each composite function?
Solution (i)
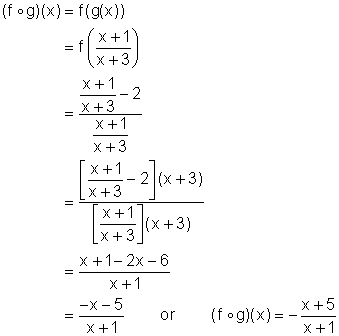
The composite function is a rational expression and we learned about the replacement set for a rational expression in an earlier unit in this course. We can see from the above expression for ![]() that -1 must be excluded from its replacement set (i.e. from its domain). However, we have to also consider something else.
that -1 must be excluded from its replacement set (i.e. from its domain). However, we have to also consider something else.
The composite ![]() can not have elements in its domain for which the function g is not defined. If we look at g we see that -3 must be excluded from its replacement set (domain). Putting both of these facts together we have:
can not have elements in its domain for which the function g is not defined. If we look at g we see that -3 must be excluded from its replacement set (domain). Putting both of these facts together we have:
Domain ![]() = {x | x ¹ -1 and x ¹ -3}
= {x | x ¹ -1 and x ¹ -3}
Solution (ii)
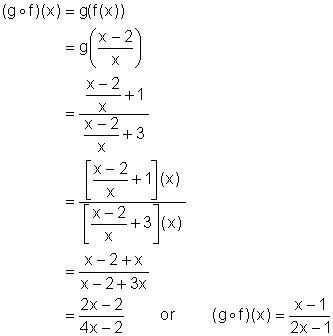
We can see from the above expression for ![]() that
that ![]() must be excluded from its replacement set (i.e. from its domain).
must be excluded from its replacement set (i.e. from its domain).
The composite ![]() can not have elements in its domain for which the function f is not defined. If we look at f we see that 0 must be excluded from its replacement set (domain). Putting both of these facts together we have:
can not have elements in its domain for which the function f is not defined. If we look at f we see that 0 must be excluded from its replacement set (domain). Putting both of these facts together we have:
Domain ![]() =
= ![]()
Example 4
(a) If f(x) = ![]() and g(x) =
and g(x) = ![]() , find (i) (
, find (i) (![]() )(x) ; (ii) (
)(x) ; (ii) (![]() )(x), and give the domain of each.
)(x), and give the domain of each.
(b) Find (![]() )(5) two different ways.
)(5) two different ways.
Solution (a)(i)

The above expression for ![]() contains a square root in the numerator and we know that we can only find the square root of a non-negative number. Thus:
contains a square root in the numerator and we know that we can only find the square root of a non-negative number. Thus:
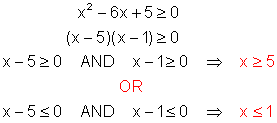
But the expression for ![]() is also rational with denominator x - 1 so we must exclude 1, or the denominator will be zero. We can accommodate this by altering the second condition above to x < 1.
is also rational with denominator x - 1 so we must exclude 1, or the denominator will be zero. We can accommodate this by altering the second condition above to x < 1.
Now consider the domain of g (the "inside" function). We must exclude any values for which it is not defined, since we cannot find f for a non-existent value. Looking at g, we see that it is undefined at 1, and this is already taken into account by our other conditions. Thus we have:
Domain ![]() = {x | x < 1 or x ³ 5}
= {x | x < 1 or x ³ 5}
Solution (a) (ii)
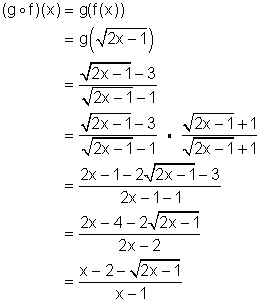
The above expression for ![]() contains a square root in the numerator and we know that we can only find the square root of a non-negative number. Thus:
contains a square root in the numerator and we know that we can only find the square root of a non-negative number. Thus:
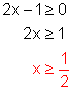
But the expression for ![]() is also a fraction with denominator x - 1 so we must exclude 1, or the denominator will be zero. Thus x ¹ 1.
is also a fraction with denominator x - 1 so we must exclude 1, or the denominator will be zero. Thus x ¹ 1.
Now consider the domain of f (the "inside" function). We must exclude any values for which it is not defined, since we cannot find g for a non-existent value. Looking at f, we see that its domain is already assumed by our first condition. Thus we have:
![]()
Solution (b)
Finding each function in turn or Using (![]() )(x) above
)(x) above
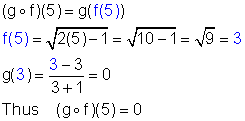
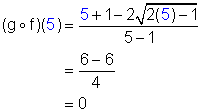
We can find a particular range value of a composite function by considering the graphs of the functions used to compose it. This is shown in the following example.
Example 1
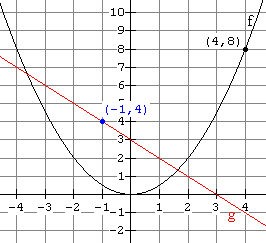
Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
(a) What is (![]() )(-2)
)(-2)
(b) What is (![]() )(0)
)(0)
(c) What is (![]() )(2)
)(2)
(d) What is (![]() )(-1)
)(-1)
Solution
|
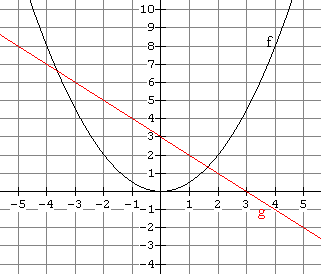
(a) ( From the graph of f, we see that f(-2) is 2. Now use x = 2 and the graph of g to find g(2) which is 1. Thus ( |

|
|
(b) ( From the graph of f, we see that f(0) is 0. Now use x = 0 and the graph of g to find g(0) which is 3. Thus ( |
|
|
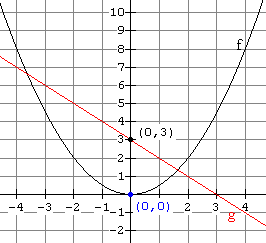
(c) ( From the graph of g, we see that g(2) is 1. Now use x = 1 and the graph of f to find f(1) which is Thus ( |
|
|
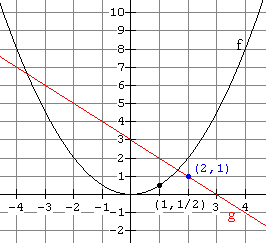
(c) ( From the graph of g, we see that g(-1) is 4. Now use x = 4 and the graph of f to find f(4) which is 8. Thus ( |
 |
Activity
For exercises 1 - 7 find (a) (![]() )(x) (b) (
)(x) (b) (![]() )(x), and give the domain of each.
)(x), and give the domain of each.
1. f(x) = x + 3 and g(x) = 2x + 5
2. f(x) = x2 + 3x + 2 and g(x) = x - 1
3. f(x) = ![]() x and g(x) = 40x - 10
x and g(x) = 40x - 10
4. f(x) = x3 and g(x) = x + 1
5. f(x) = ![]() and g(x) = x
and g(x) = x
6. f(x) = ![]() and g(x) = x3 + 2x
and g(x) = x3 + 2x
7. f(x) = ![]() and g(x) =
and g(x) = ![]()
8. Find ![]() if f(x) = x - 1, g(x) =
if f(x) = x - 1, g(x) = ![]() , and h(x) = x2
, and h(x) = x2
9. Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
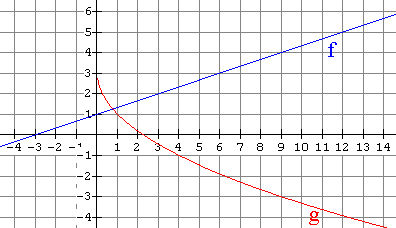
(a) What is (![]() )(9)
)(9)
(b) What is (![]() )(0)
)(0)
(c) What is (![]() )(9)
)(9)
Test Yourself
For exercises 1 - 4 find (a) (![]() )(x) (b) (
)(x) (b) (![]() )(x), and give the domain of each
)(x), and give the domain of each
1. f(x) = 4x - 3 and g(x) = -2x + 5
2. f(x) = 2x + 3 and g(x) = 2x2 - 1
3. f(x) = ![]() and g(x) =
and g(x) = ![]()
4. f(x) = ![]() and g(x) =
and g(x) = ![]()
5. Find ![]() if f(x) =
if f(x) = ![]() , g(x) =
, g(x) = ![]() , h(x) = x2 - 1
, h(x) = x2 - 1
6. Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
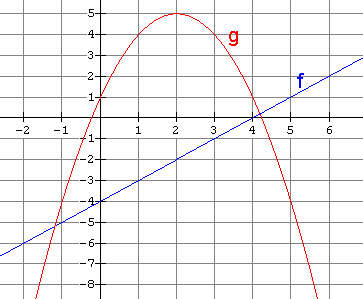
(a) What is (![]() )(3)
)(3)
(b) What is (![]() )(6)
)(6)
(c) What is (![]() )(0)
)(0)
(d) What is (![]() )(4)
)(4)