Learning Resources
Outcomes
By the end of this lesson you will be able to answer questions like the ones in the pre-test below.
Approach #1
Answer the questions on the pre-test below in your Math 3103 binder. Then refer to the pages of the lesson that contain instruction on the questions you were unable to do, for which you got an incorrect answer, or for which you would like some further explanation.
Approach #2
Proceed directly to the first page of the lesson without attempting the pre-test. To do this simply click on the Lesson button above. You can then return to this pre-test later and use it as a worksheet.
Pre-test
For exercises 1 - 5 find (a) (
)(x) and (b) (
)(x)
1. f(x) = 3x and g(x) = 2x - 5
2. f(x) = 7x - 2 and g(x) = 6x2 - 1
3. f(x) = 4x - 5 and 
4. f(x) = 
and g(x) = 
5. f(x) = 
and g(x) = 
6. For f(x) =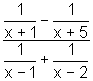 
and g(x) = x2 , find (a) ()(3) , (b) ()(3)
7. Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
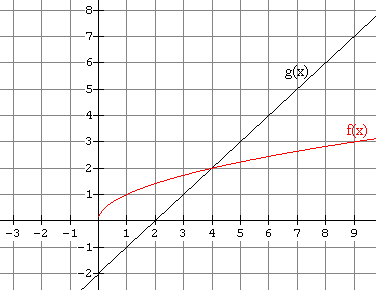
(a) What is ()(1)
(b) What is ()(9)
(c) What is ()(1)
(d) What is ()(6)
8. State the domain of each of the composite functions in exercises 1 to 5 above.
Students will be expected to:
- Given two functions f(x) and g(x), find the composite rules
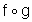(x) and
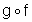(x). - Perform calculations involving the composite of two functions in either algebraic of graphical form.
- Find the inverse of a linear or quadratic function and determine whether the inverse is a function.
- Sketch the graph of an inverse function by interchanging coordinates.
Introduction
This section consists of four lessons as follows:
Lesson 01 Composition of Functions
In this lesson you will study the concept of the composition of functions. You will learn the notation for composite functions and how to find for given functions f and g. You will also calculate (x) for particular functions when they are given in algebraic or graphical form.
Lesson 02 Inverse Functions Defined
In this lesson you will learn the definition of inverse functions. You will see how inverse functions are defined in terms of composites. You will learn how to check if two given functions are inverses of each other and how to draw the graph of the inverse by reflecting the original function in the line y = x. You will also be introduced to the inverse functional notation 
.
Lesson 03 Inverse of Linear Functions
In this lesson you will learn how to find the inverse of a given linear function by interchanging the x and y variables in the given function.
Lesson 04 Inverse of Quadratic Functions
In this lesson you will find the inverse of quadratic functions and discover that the inverse is not a function. You will learn how to restrict the domain of a given quadratic function so that its inverse is a function.
Prerequisites
To be successful in this lesson, it would be helpful to know the following:
- The definition of a function.
- The definition of and how to find the domain and range of a function.
- The various methods of describing a function, viz. "f of x" notation, graphing, and mapping diagrams.
- How to find the value of f(x) for a given value of x.
- How to substitute one expression or formula into a second expression or formula.