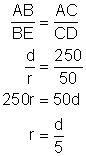Learning Resources
Lesson
Example 1
Water is being poured into a right circular conical tank as shown in the diagram below:
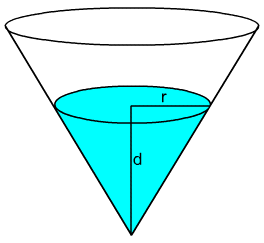
(a) Express the volume of the water in the tank at any given time as a function
of the depth of the water, d , and the radius of the tank at the surface of
the water , r .
(b) If the tank has a total depth of 250 m and a radius of 50 m, express the
volume of water in the tank as a function of d only. (Hint: draw in lines for
the total depth and radius, and use similar triangles to find a formula relating
h and d).
(c) If water flows into the tank at a rate of 5000 m3 per minute, what is the depth of the water after (i) 15 min, (ii) 30 min , (iii) 1 hour
Solution
(a) Since the shape of the water is that of a right circular cone, its volume is:
(b)  |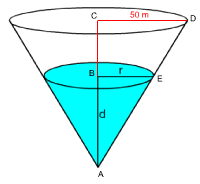
Consider DABE and DACD,
since they are similar
Substituting this expression for r into the equation in part (a) we get:
|
(c) Rearranging the formula in part (b) to solve for d we get:
(i) Volume after 15 min = 15 min x 5000 m3/min = 75 000 m3 Using the formula above for d, we get:
(ii) Volume after 30 min = 30 min x 5000 m3/min = 150 000 m3 Using the formula above for d, we get:
(iii) Volume after 1 h = 60 min x 5000 m3/min = 300 000 m3 Using the formula above for d, we get:
Challenge: Use a spread sheet or some other technology to create a table of
values of depth of water versus time for 10 min intervals. Construct a
graph of the data and interpret the graph in terms of the rate at which
the depth is changing.
Example 1
A plane leaves Deer Lake and travels north at the rate of x km/h. At the same time, a second plane leaves Deer Lake and travels east at the rate of y km/h. (Hint: sketch a diagram to help answer the following questions)
(a) Express the distance between the planes, d , as a function of x, y ,and the time, t, since they have left.
(b) If the second plane is traveling 50 km/hr faster that the first, express d as a function of x and t.
(c) If the first plane is traveling 300 km/h, how far apart are they after 2 hours?
Solution
(a) Sketch a diagram showing the relative positions of the two planes:
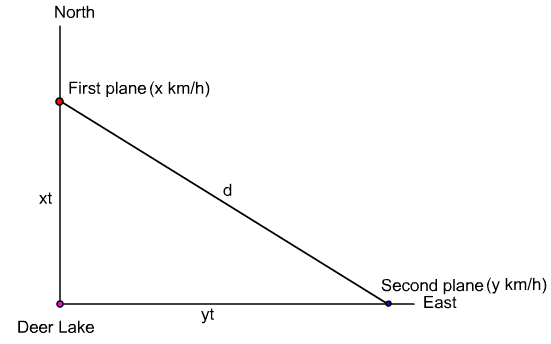
(a) Distance traveled by first plane in x hours = (rate)(time) = xt
Distance traveled by second plane in x hours = (rate)(time) = yt
Using the Pythagorean Theorem we get:
(b) Since the second plane is traveling 50 km/h faster than the first, we have:
y = x + 50
Substituting this expression for y into the equation in part (a) we get:
(c) Substituting x = 300 km/h and t = 2 h into the equation in (b) we get:
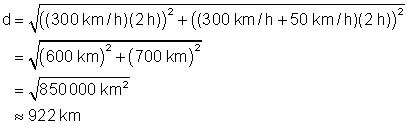
Example 1
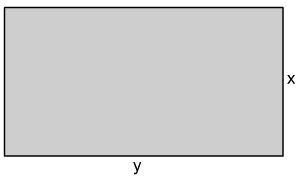
A rectangular piece of sheet metal is x metres wide by y metres long:
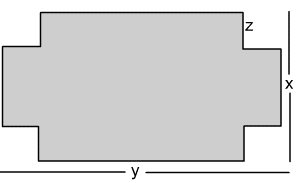
It has congruent squares with sides z metres cut from the corners:
The edges are then turned up along the red lines to make an open box with no top.
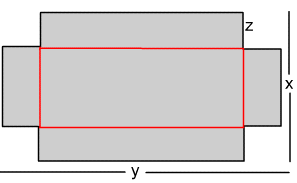
(a) Express the volume of the box, V , as a function of x , y , and z.
(b) If the length is 7 m more than the width, express V as a function of x and z.
(c) If the width of the piece of metal is 8 m, what are the dimensions of the square that has to be cut out to give the box a volume of 88 m3 ?
Solution
(a) Length of the base of the box = y - 2z
Width of the base of the box = x - 2z
Height of the box = x
Volume of box = (Length)(Width)(Height)
V = (y - 2z)(x - 2z)(z)
(b) Since the length is 7 more than the width, we have: y = x + 7 Substituting this expression into the formula in part (a) we get:
V = (x - 2z + 7)(x - 2z)(z)
(c) Substituting 8 for x, and 88 for V in the formula in part (b) we get:
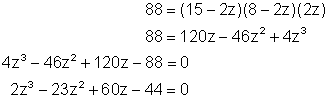
We now apply the rational roots theorem to find the value of z. However, since
z is a length, we need only consider the positive values. Possible positive
rational roots are: 
. Also, because z must be
less than 4 (half the width), we need only consider 
. Use either
synthetic division or substitution to determine which, if any of these possible
roots are actual roots.
z = 
-> 
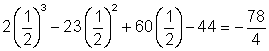; hence is not a root.
z = 1 -> 2(1)3 - 23(1)2 + 60(1) - 44 = - 5 ; hence 1 not a root.
z = 2 -> 2(2)3 - 23(2)2 + 60(2) - 44 = 0 ; hence 2 is a root.
Dimensions of the square to cut out are 2 by 2.
Activity
1. Water is being poured into a trough in the shape of a triangular prism as shown in the diagram below.
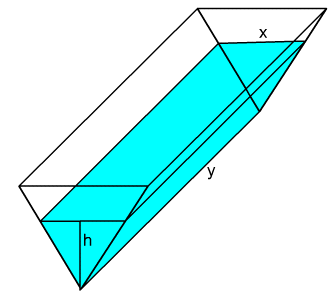
(a) Express the volume of water in the trough at any given time as a function of h , x , and y, where h is the water depth, x is the width of the trough at water level, and y is the length of the trough.
(b) If the depth of the trough is 20 m, the width of the trough is 30 m, and the length of the trough is 50 m express the volume of water in the trough as a function of h only.
(c) If water is poured in at the rate of 500 m3/min., what is the depth after: (i) 5 min. , (ii) 10 min. , (iii) 20 min. ?
2. Plane A leaves St. John's at noon and travels north at the rate of x km/h. At the same time, plane B is 800 km east of St. John's and traveling west at y km/h. Press the show button to see an animation of this:
(a) Express the distance, d , between plane A and B as a function of x , y and t, where t is the number of hours after noon.
(b) If plane B is traveling 40 km/h faster than plane A, express d as a function of t and x.
(c) If plane A is traveling 290 km/h, how far apart are the planes after 2 hours?
3. A rectangular solid has length x units, width y units, height h units, and diagonal d units as shown in the diagram below.
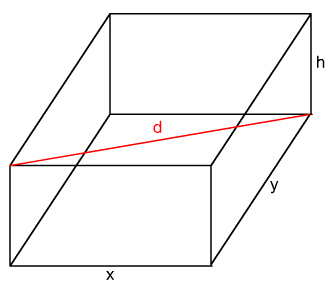
(a) Express d as a function of x , y, and h .
(b) If the base is a square, and d, the diagonal of the box in the formula in part (a) is 10 units, express the height as a function of the width.
Test Yourself
1. A greenhouse is h metres high and L metres long with its roof in the shape of a
semicircle as shown in the diagram below.
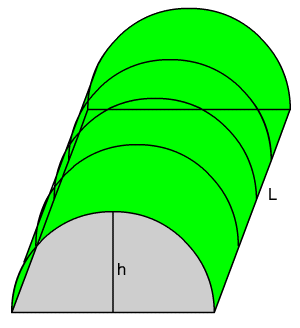
(a) Express the volume, V , as a function of h and L
(b) If it takes 400 m2 of plastic to cover the top and two ends, including any doors and windows, express V as a function of h only.
(c) What is the volume of the greenhouse if the height is 4 metres?
2. Plane A leaves Stephenville headed north at the rate of x km/h. Two hours later, plane B leaves Stephenville headed east at the rate of y km/h.
(a) Express the distance, d , between the planes t hours after plane B leaves as a function of x , y , and t.
(b) If plane B is traveling 50 km/h faster than plane A, express d as a function of x and t.
(c) If plane A travels at 200 km/h, how long after B leaves will they be 1250 km apart?