Learning Resources
Lesson
This lesson deals with how to express functions of two variables as functions of one variable. The process involves writing two formulas and then rearranging one of them to solve for a certain variable. The value of that variable is then substituted into the other formula. Those of you who have solved system of equations by the substitution method will already be familiar with the process.
Example 1
The length of a rectangle is x units and its width is y units, as shown in the diagram below.
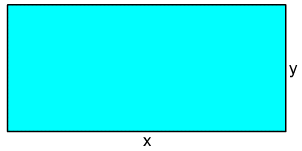
(a) Express the area, A, as a function of the length and width.
(b) If the length is twice the width, express the area, A, as a function of: (i) the width , (ii) the length.
Solution
(a) The formula for the area of a rectangle is: Area = (length)(width). This gives:
A = xy
(b) (i) It is given that the length is twice the width, thus x = 2y. Substitute this expression for x into the equation in part (a) to get,
A = xy = (2y)y or A = 2y2
(b)(ii) Solve the formula x = 2y for y. This gives: y = 
. Substitute this expression
for y into the equation in part (a) to get,
A = xy = 
or A = 
Example 1
A box has a square base, x metres on a side, and a height of y metres, as shown in the diagram below.
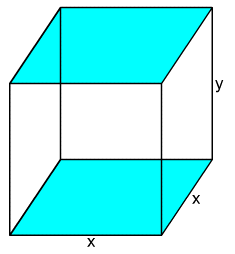
(a) Express the volume, V, as a function of x and y.
(b) If the total surface area of the box is 6 m2 , express the volume as a
function of x.
Solution
(a) The formula for the volume of a right prism is V = (area of base)(height). Applying this formula to the above figure we get:
V = (x2)(y) =x2y
(b) Since we wish to express V as a function of x only, we need to eliminate y in
the above formula.
The total surface area of the box is the area of top and bottom plus the area of
the four sides.
Total Surface Area = 2x2 + 4xy
But we are given that the total surface area is 6 m2 , thus we have:
2x2 + 4xy = 6
Solving this formula for y gives:
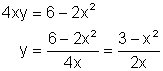
Substituting this value for y into the formula in part (a) gives:
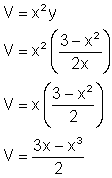
Example 1
In the diagram below, the vertices of the rectangle ABCD are on the x-axis and on the parabola.
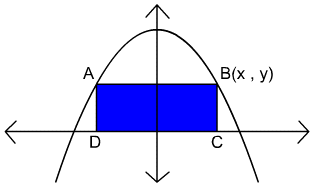
(a) Express the area, A, of the rectangle ABCD as a function of x and y.
(b) If the equation of the parabola is y = 12 - x2 , express the area A as a
function of: (i) x , (ii) y
Solution
(a) The formula for the area of a rectangle is: Area = (length)(width). Applying this formula to the rectangle ABCD we get:
A = (2x)(y) or A = 2xy
(b)(i) Since we wish to express A as a function of x only, we need to eliminate y in the above formula.
Since vertex B of the rectangle lies on the parabola, x and y must satisfy the relation expressed by the equation of the parabola. Thus we have:
y = 12 - x2
Substituting this value for y into the equation in part (a) we get:
A = 2xy = 2x(12 - x2) or A = 24x - 2x3
(b)(ii) Since we wish to express A as a function of y only, we need to eliminate x in the above formula.
Since vertex B of the rectangle lies on the parabola, x and y must satisfy the relation expressed by the equation of the parabola. Thus we have:
y = 12 - x2
Solving this formula for x we get:
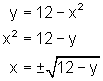
If you forget the reason for the ± in the above solution, review your work on on solving quadratic equations which we did in this course. However, from the diagram, x is clearly positive, thus we can write 
.
Substituting this value for x into the equation in part (a) we get:
A = 2xy = 
or A = 
Activity
1. The length of a rectangle is x units and its width is y units
(a) Express the area, A , as a function of the length and width.
(b) If the perimeter of the rectangle is 100 cm , express A as a function of (i) x , (ii) y. (Hint: Sketch a diagram similar to the one in the Pre-test)
2 A rectangular plot is to be fenced and divided into three pens as shown in the diagram below.
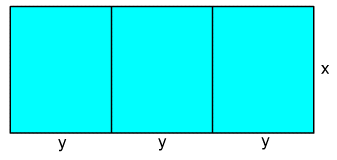
(a) Express the area of the plot, A , as a function of x and y.
(b) If the entire job will use 240 m of fencing, express the area, A , as a function of (i) x , (ii) y
3. A box has a rectangular base, x metres wide and 2x metres long, and a
height of y metres:
(a) Express the Total Surface Area, S , as a function of x and y.
(b) If the volume of the box is 8 m3 , express S as a function of: (i) x , (ii) y
4. A right circular cylinder has radius r metres and height h metres as shown in the diagram below:
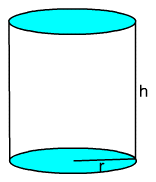
(a) Express the total surface area, S , as a function of r and h.
(b) If the volume of the cylinder is 10 m3 , express S as a function of: (i) r , (ii) h
5. In the diagram below, the vertices of the rectangle ABCD are on the x-axis and on the circle as shown:
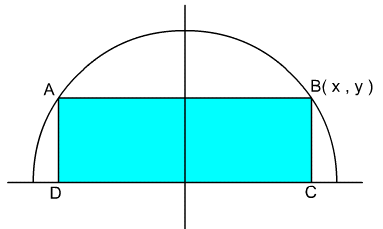
(a) Express the area, A, of the rectangle ABCD as a function of x and y.
(b) If the equation of the circle is x2 + y2 = 36, express the area A as a function of x.
6. In the diagram below, the vertices of the trapezoid are on the x-axis and on the parabola, with coordinates as shown:
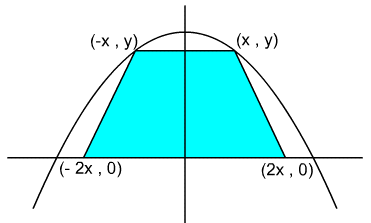
(a) Express the area, A, of the trapezoid as a function of x and y.
(b) If the equation of the parabola is y + x2 = 10, express the area A as a function of: (i) x , (ii) y.
Test Yourself
1. A trapezoid has dimensions as shown below:
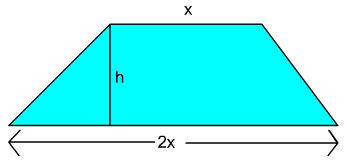
(a) Express the area, A , as a function of x and h.
(b) If the height, h , is 
the shorter base, express A as a function of: (i) x , (ii) h
2. A right circular cylinder has radius r metres and height h metres as shown in the diagram below:
(a) Express the volume, V , as a function of r and h.
(b) If the total surface area of the cylinder is 10 m2 , express V as a function of: r
3. In the diagram below, the vertices of the triangle ABC are on the x-axis and y-axis, and on the ellipse as shown:
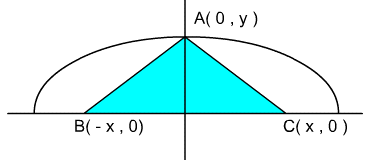
(a) Express the area, A, of the triangle ABC as a function of x and y.
(b) If the equation of the ellipse is x2 + 4y2 = 36, express the area A as a function of: (i) x , (ii) y .