Learning Resources
Lesson
In Section 01 of this Unit we solved equations which contained rational expressions. We are now going to apply those skills to rearranging formula which contain rational expressions.
Recall that there were several approaches to take to solving these equations. Pick the one that best matches the given problem. The three examples below each use a different approach.
Example 1
Solve 
for R
Solution
Example 2
Solve 
for D
Solution
Example 3
Solve 
for a
Solution
In Unit 03 of this course we solved equations which contained radical expressions. Example 1 applies those skills to rearranging a formula which contains a radical expression.
Example 1
Solve 
for m
Solution
Sometimes the variable we wish to solve for is raised to a power. In that case we isolate the term containing the variable and then find the appropriate root of each side. This is shown in Example 2 below.
Example 2
Solve 
for r
Solution
One of the reasons for rearranging a formula and making a particular variable the subject is so that we can find the value of that variable for certain given information. This is shown in Example 1 below.
Example 1
The formula for the volume of a sphere with radius r is 
. Rearrange the formula and solve for r. Then find the radius necessary to give a volume of one litre.
Solution
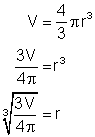
Volume = 1 L = 1000 cm3 . Substitute this into the formula.
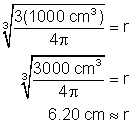
Activity
Solve each of the formulas in exercises 1 - 7 for the variable indicated:
1. 
for t
2. 
for q ; for r
3. 
for t
4. 
for R
5. 
for R
6. 
for t1
7. 
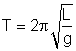for g
8. The force, F , between two objects with masses m1 and m2 at a distance of d units apart is given by the formula 
, where k is some constant. Solve the formula for d and use it to find the distance between two objects where the force is 240, the masses 20 and 30, and the constant 10.
Test Yourself
Solve each of the formulas in exercises 1 - 6 for the variable indicated:
1. 
for r
2. 
for x
3. 
for Z2
4. 
for r
5. 
for r
6. 
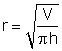for h