Learning Resources
Lesson
A formula is an equation giving the relation between two or more quantities in the real world. For example the area of a triangle with base, b, and height ,h is given by the formula, A= 
bh.
Because formulas are equations, all the principles of equations apply to rearranging formula. That is we can add or subtract the same quantity from both sides of a formula, or we can multiply and divide both sides of the formula by the same quantity, and we obtain an equivalent formula. This is shown in the following examples:
Example 1
Solve A= bh, for h
Solution
Quite often it is necessary to use more than one of the principles of equality in order to rearrange a formula. It is then important to know which step to do first. This is shown in the following example.
Example 2
Solve p = 2L + 2W, for W
Solution
Sometimes the variable we wish to solve for is contained inside a bracket as in Example 1 below. We then eliminate everything outside the bracket first and proceed from there.
Example 1
Solve 
Solution
Another situation that arises is that sometimes the variable we wish to solve for is contained in two or more terms in the formula. In that case we generally have to factor before we apply the properties of equality. This is shown in Example 2 below.
Example 2
Solve 
for h
Solution
One of the reasons for rearranging a formula and making a particular variable the subject is so that we can find the value of that variable for certain given information. This is shown in Example 1 below.
Example 1
The formula for the total surface area of a rectangular solid below, which has square base of side s units long and height of h units, is A = 2s2 + 4sh.
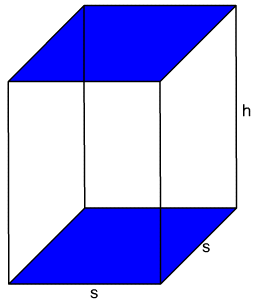
(a) Rearrange the formula and solve for h.
(b) Use this rearranged formula to find the height necessary to give a total surface area of 500 cm2 when the base is 5 cm on a side.
(c) Use this rearranged formula to find the height necessary to give a total surface area of 1500 cm2 when the base is 5 cm on a side.
Solution
(a)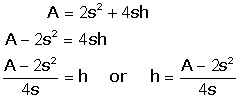 
(b)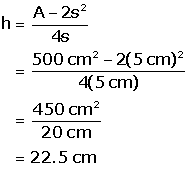 
(c)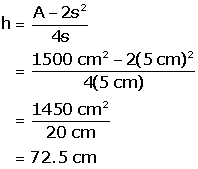 
Activity
Solve each of the formulas in exercises 1 - 7 for the variable indicated:
1. 
for h
2. 
for F
3. 
for h
4. 
for A
5. 
for m
6. pr + pq = s for p
7. ax + b = ay + q for a
8. The formula for the total surface area of the cylinder below, which has radius r
and height h, is given by the formula 
.
(a) Rearrange the formula and solve for h.
(b) Find the height if the surface area is 100 cm2 and the radius is 3 cm.
(c) Find the height if the surface area is 50 cm2 and the radius is 1.5 cm.
(d) Find the height if the surface area is 150 cm2 and the radius is 
cm.
Test Yourself
Solve each of the formulas in exercises 1 - for the variable indicated:
1. 
for r
2. 
for h
3. 
for d
4. for n
5. 
for g
6. y - mx = y1 - mx1 for m