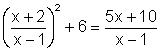Learning Resources
Lesson
There are several approaches that may be taken to solving equations that contain rational expressions. One is to use the multiplication property of equality that you learned in earlier courses. It states:
if x = k, then ax = ak
In equations containing rational expressions, the value of "a" that is used for the multiplication is the LCD of all the fractions in the equation. As you will see from the examples below, this effectively eliminates the rational expressions from the equation and we proceed to solve the resulting equation in the usual way.
Example 1
Solve: ![]()
Solution (Method 1)
Although the working is not shown in the above example, you should always substitute the answer you obtain back into the original equation. This is to check that you have a correct solution and to check for extraneous roots.
Another approach that can be used to solve equations that contain rational expressions is to use the "cross multiplication" property for ratios. This property states,
![]()
In order to use this method you must have a single rational expression on both sides of the equality sign. If there are several fractions or other expressions, they must first be combined using the skills learned in the earlier lessons of this unit. Solving Example 1 above by this method we get:
Solution (Method 2)
Which method you use is entirely up to you. If the equation is already set up with single fractions on both sides, Method 2 is the easier to use. Otherwise it is probably easier to stick with Method 1.
In Lesson 01 of this unit we talked about the replacement set for rational expressions. When solving equations, we have to be very aware of this replacement set. In Example 1 on the previous page, we know that the value of x cannot be - 2, as this would make the denominator zero. If the solution to the equation had contained - 2 as an answer, it would have been excluded. It would be an extraneous root; that is, a root of the final equation that does not work in the original equation.
We saw extraneous roots in a different context in Unit 03 of this course where we solved radical equations. We will now look at them in the context of rational equations.
The following example illustrates the problem of extraneous roots.
Example 1
Solve: ![]()
Solution
There are methods of solving equations that contain rational expressions other than the two we have used so far.
A property of fractions that may be used to solve equations containing rational expressions states that if two fractions are equal and have the same denominator, then their numerators must also be equal. That is:
![]()
This property is used to solve the following example.
Example 1
Solve: ![]()
Solution:
So far all the examples have resulted in solving a linear equation once the rational expressions have been eliminated. It is possible that the resulting equation is not linear and must be solved using the techniques we learned in Unit 03. The next example illustrates this type of problem. You can still use any of the three methods to solve it
Example 2
Solve: ![]()
Solution
Activity
Solve the following equations.
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()
Test Yourself
Solve the following equations.
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()