Learning Resources
Lesson
A complex fraction is one whose numerator or denominator, or both, contains either:
(i) one or more fractions or,
(ii) powers with negative exponents.
For example,
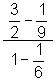 and
and ![]()
are complex fractions.
There are two methods of simplifying complex fractions.
Method 1: Express the fraction as a quotient using the sign ¸
Method 2: Multiply the numerator and denominator by the LCD of all the fractions
within the numerator and denominator.
Example 1
Simplify: 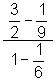
Solution (Method 1)
Solution (Method 2)
Example 2
Simplify: ![]()
Solution (Method 1)
Solution (Method 2)
Example 3
Simplify: 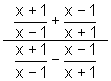
Solution (Method 1)
Solution (Method 2)
Example 4
Simplify: 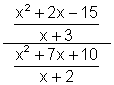
Solution (Method 1)
Solution (Method 2)
Although each of the examples above are solved by both methods, it is left to you to pick the method that you follow best or that best suits a given complex fraction.
We can apply the concepts and operations associated with rational expressions to various problem solving situations similar to that presented in Question 7 on the pre-test.
In order to answer some of these questions you will need to recall the formulas for areas and volumes of various geometric figures.
Example 1
A sphere of radius x is to be fit into a cubical container for shipping. If the sphere just touches the sides of the container in which it is placed, what fraction of the volume of the container is not used by the sphere?
Solution
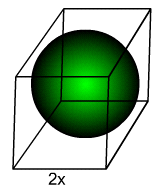
The volume of the cube = (2x)(2x)(2x) = 8x3
The volume of the sphere = ![]()
Volume not used = 8x3 - ![]()
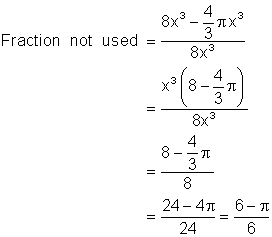
Activity
Simplify each of the complex fractions in exercises 1 to 12.
1. ![]() 2.
2. 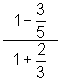 3.
3. 
4. 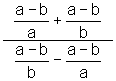 5.
5. 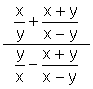 6.
6. 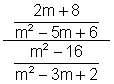
7. 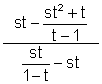 8.
8. 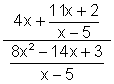 9.
9. 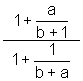
10. ![]() 11.
11. ![]() 12.
12. 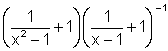
13. What fraction of the rectangle ABCD is shaded?
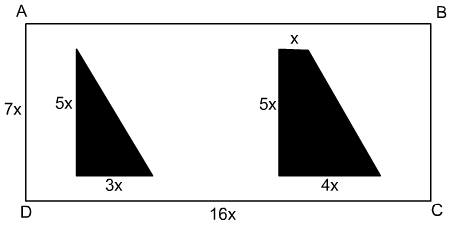
Test Yourself
Simplify each of the complex fractions in exercises 1 to 6.
1. 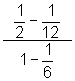 2.
2. 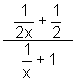 3.
3. 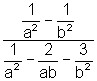
4. 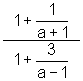 5.
5. 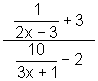 6.
6. ![]()
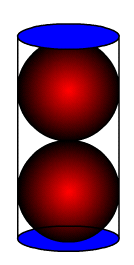
7. If the two balls pictured in the container below just touch the sides of the container, what fraction of the volume of the container is unused by the two balls? (Hint: let the radius of the balls be r).