Learning Resources
Lesson
You learned in previous mathematics courses that the denominator of a fraction cannot be zero because division by zero is impossible. When the denominator contains an algebraic expression, the values that make the denominator equal to zero must be excluded from the replacement set. This is shown in the following examples.
Example 1
What values must be excluded from the replacement set of 
?
Solution
The method of Example 1 works for all rational expressions. The only difference is in the degree of difficulty and type of equation you have to solve.
Example 2
What values must be excluded from the replacement set of 
Solution
A rational expression is in lowest terms, also called simplest or standard form, if the greatest common factor of the numerator and denominator is 1.
Thus to reduce an algebraic fraction to lowest terms, first factor the numerator and denominator completely. Then look for the common factors which will reduce to 1.
Example 1
Reduce to lowest terms:
Solution:
The reduced form of the rational expression must always give the same value as the original expression for every number from the replacement set substituted in for the variable. In Example 1 above, if we substitute x = 5 into the original and reduced forms we get:
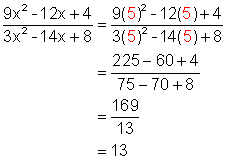
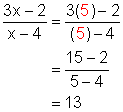
Note that both answers are the same.
However, remember the numbers that must be excluded from the replacement set. In Example 1 above, one of the numbers that must be excluded from the replacement set is 
. If that is substituted into the original and reduced form we get:
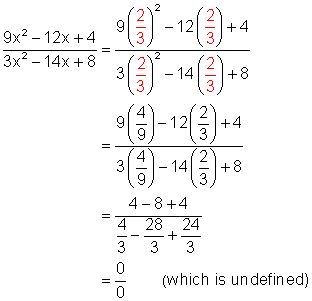
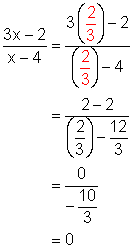
Note that the answers are different. Remember this as it will become very important in a later lesson where we solve equations involving rational expressions.
Example 2
Reduce to lowest terms: 
Solution
Activity
Reduce to lowest terms and give the values that must be excluded from the replacement set.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
Test Yourself
Reduce to lowest terms and give the values that must be excluded from the replacement set.
1. 
2. 
3. 
4. 
5. 
6. 