Learning Resources
Lesson
Single Radical
An equation that has a variable in a radicand is called a radical equation. Examples of radical equations are:
; 
; 
; 
To solve an equation having a term with a variable in a radicand, start by "isolating" such a term on one side of the equation. Then raise the expression on each side of the equal sign to a power equal to the index of the radical. This is shown in the examples below.
Example 1
Solve: 
Solution
Example 2
Solve: 
Solution
In Examples 1 and 2 above we checked our solution. Why are we doing this now, whereas in our previous work on finding the roots of equations (quadratics, cubics, quartics) we did not stress the necessity of checking our solutions?
Actually, checking solutions is a good practice to follow regardless of the type of equation you are solving. We should have done it when solving these other equations too. However, it is especially important to check solutions when solving radical equations because of the process of squaring both sides. The process of squaring can introduce unacceptable or extraneous roots. An example of this is shown in the following sequence:
Because squaring can introduce these extraneous roots, it is essential we check the solutions we find to any equation that involves squaring both sides.
Example 3
Solve: 
Solution
Multiple Radicals
Sometimes, a radical equation contains more than one term with a variable in a radicand. When this happens, you have to "isolate and raise to a power" more than once. Generally speaking it is better to isolate the more complicated radical first, as this can simplify the process of raising the expressions to a power.
Example 1
Solve: 
Solution
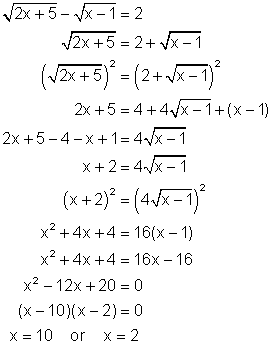
Check: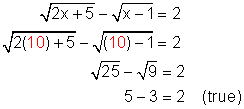 
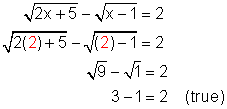
So the solution is x = 10 and x = 3
Example 2
Solve: 
Solution
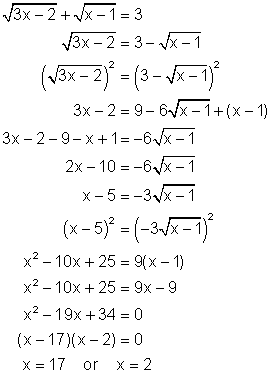
Check: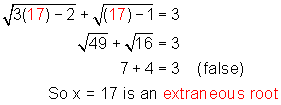 
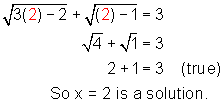
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Solve each of the following equations:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
Test Yourself
Solve each of the following equations:
1. 
2. 
3. 
4. 
5. 
6. 
7. 