Learning Resources
Lesson
Constant Functions
All constant functions can be written in the form f(x) = k, where k Î R .
To write the equation or function notation for a particular constant function we need only determine the particular value of k for that function. This can be read from the graph or the y-coordinate of any point on the graph (since all points have the same y-coordinate).
Example 1
Write the function notation for the graph shown below.
Solution
Since the y-intercept is 10, one point on the graph is (0 , 10). The value of k is thus 10. The function notation is: f(x) = 10.
It should be obvious that this particular constant function has no real zeros (no x-intercepts). The only constant function with real zeros is the line f(x) = 0, and it has infinitely many zeros.
Linear Functions
All linear functions can be written in the form f(x) = a(x - h), where a and h Î R , h is the real zero and a, the leading coefficient, determines the "stretch" factor and if there is a reflection across the x-axis.
To write the equation or function notation for a particular linear function using this method, we need its zero and some way of determining the value of a. Usually this is found by substituting in the coordinates of some point on the graph other than the zero.
Example 1
Write the function notation for the graph shown below.
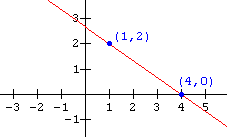
Solution
Since the graph is that of a linear function (straight line), we can write it as:
f(x) = a(x - h)
From the graph (i.e. from the x-intercept), we see that the zero of the function is x = 4 . Thus the equation becomes:
f(x) = a(x - 4)
To determine the value of a, substitute in the coordinates of the point (1 , 2) which is on the graph:
2 = a(1 - 4)
2 = - 3a
a = - ![]()
The function notation for the graph is thus: f(x) = - ![]() (x - 4)
(x - 4)
Quadratic Functions
If a quadratic function has two real zeros, then it can be written in the form f(x) = a(x - h)(x - k) , where a , h, k Î R . h and k are the real zeros, and a, the leading coefficient, determines the "stretch" factor and if there is a reflection across the x-axis.
To write the equation or function notation for a particular quadratic function using this method, we need its real zeros and some way of determining the value of a. Usually this is found by substituting in the coordinates of some point on the graph other than the zero.
Example 1
Write the function notation for the graph shown below.
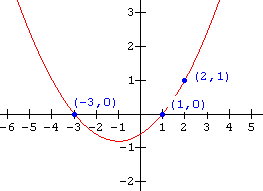
Solution
Since the graph is a quadratic (a parabola), its function may be written as:
f(x) = a(x - h)(x - k)
From the graph (the x-intercepts) we see that the zeros are x = - 3 and x = 1. Thus the equation becomes:
f(x) = a( x + 3)(x - 1)
To determine the value of a, substitute in the coordinates of the point (2 , 1) which is on the graph:
1 = a(2 + 3)(2 - 1)
1 = 5a
a = ![]()
The function notation for the graph is thus: f(x) = ![]() (x + 3)(x - 1)
(x + 3)(x - 1)
Example 2
Write the function notation for the graph shown below.
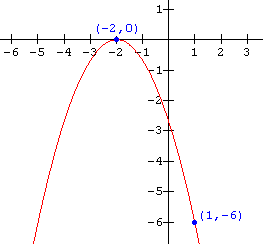
Solution
Since the graph is a quadratic (a parabola), its function may be written as:
f(x) = a(x - h)(x - k)
From the graph (the x-intercepts) we see that the function has two identical zeros; they are
x = - 2, thus the equation becomes:
f(x) = a( x + 2)(x + 2) or f(x) = a(x + 2)2
To determine the value of a, substitute in the coordinates of the point (1 , - 6) which is on the graph:
-6 = a(1 + 2)2
- 6 = 9a
a = - ![]()
The function notation for the graph is thus: f(x) = - ![]() (x + 2)2
(x + 2)2
Note: The functions in both examples above each had two real roots. In Example 1 they were distinct, and in Example 2 they were identical. We saw in the last lesson that it is possible for a quadratic to have no real roots (an hence its graph has no x-intercepts). Such a quadratic has complex roots. We will not be determining the function notation for this type of graph in this course. The graph below of one example of this type of quadratic is given for reference only.
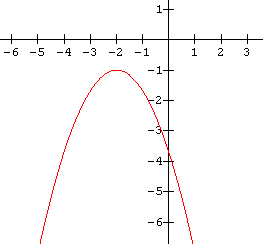
Cubic Functions
If a cubic function has three real zeros, then it can be written in the form
f(x) = a(x - h)(x - k)(x - j) , where a , h, k , j Î R . h , k , and j are the real zeros, and a, the leading coefficient, determines the "stretch" factor and if there is a reflection across the x-axis.
To write the equation or function notation for a particular cubic function using this method, we need its real zeros and some way of determining the value of a. Usually this is found by substituting in the coordinates of some point on the graph other than the zero.
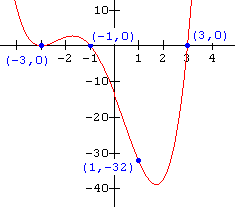
Example 1
Write the function notation for the graph shown below.
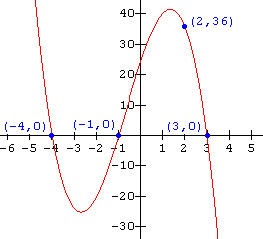
Solution
Since the graph is a cubic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)
From the graph (the x-intercepts) we see that the zeros are x = - 4 , x = - 1, and x = 3 . Thus the equation becomes:
f(x) = a( x + 4)(x + 1)(x - 3)
To determine the value of a, substitute in the coordinates of the point (2 , 36) which is on the graph:
36 = a(2 + 4)(2 + 1)(2 - 3)
36 = - 18a
a = - 2
The function notation for the graph is thus: f(x) = - 2(x + 4)(x + 1)(x - 3)
Example 2
Write the function notation for the graph shown below.
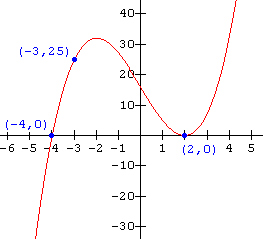
Solution
Since the graph is a cubic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)
From the graph (the x-intercepts) we see that the function has one zero are x = - 4 , and two identical zeros at x = 2 . Thus the equation becomes:
f(x) = a( x + 4)(x - 2)(x - 2) or f(x) = a( x + 4)(x - 2)2
To determine the value of a, substitute in the coordinates of the point (- 3 , 25) which is on the graph:
25 = a(- 3 + 4)(- 3 - 2)2
25 = 25a
a = 1
The function notation for the graph is thus: f(x) = (x + 4)(x - 2)2
Example 3
Write the function notation for the graph shown below.
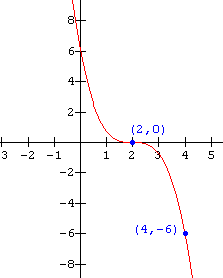
Solution
Since the graph is a cubic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)
From the graph (the x-intercepts) we see that the function has three identical zeros at x = 2 . Thus the equation becomes:
f(x) = a( x - 2)(x - 2)(x - 2) or f(x) = a(x - 2)3
To determine the value of a, substitute in the coordinates of the point (4 , -6) which is on the graph:
-6 = a(4 - 2)(4 - 2)(4 - 2)
-6 = 8a
a = - ![]()
The function notation for the graph is thus: f(x) = - ![]() (x - 2)3
(x - 2)3
Note: The functions in the examples above each had three real roots. In Example 1 they were distinct, in Example 2 there were two identical roots, and in Example 3 there were three identical roots. We saw in the previous lessons that it is possible for a cubic to have two complex roots and hence its graph will not have three x-intercepts. We will not be determining the function notation for this type of function in this course. The graph below of one example of this type of cubic is given for reference only.
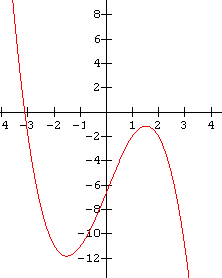
Quartic Functions
If a quartic function has four real zeros, then it can be written in the form
f(x) = a(x - h)(x - k)(x - j)(x - m) , where a , h, k , j, m Î R . h , k , j and m are the real zeros, and a, the leading coefficient, determines the "stretch" factor and if there is a reflection across the x-axis.
To write the equation or function notation for a particular quartic function using this method, we need its real zeros and some way of determining the value of a. Usually this is found by substituting in the coordinates of some point on the graph other than the zero.
Example 1
Write the function notation for the graph shown below.
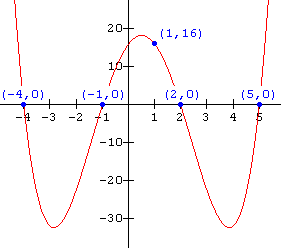
Solution
Since the graph is a quartic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)(x - m)
From the graph (the x-intercepts) we see that the zeros are x = - 4 , x = - 1, x = 2 , and x = 5 Thus the equation becomes:
f(x) = a( x + 4)(x + 1)(x - 2)(x - 5)
To determine the value of a, substitute in the coordinates of the point (1 , 16) which is on the graph:
16 = a(1 + 4)(1 + 1)(1 - 2)(1 - 5)
16 = 40a
a = ![]()
The function notation for the graph is thus: f(x) = ![]() (x + 4)(x + 1)(x - 2)(x - 5)
(x + 4)(x + 1)(x - 2)(x - 5)
Example 2
Write the function notation for the graph shown below.
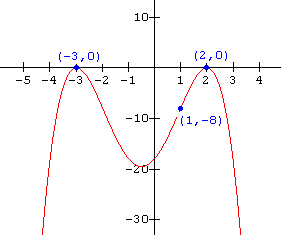
Solution
Since the graph is a quartic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)(x - m)
From the graph (the x-intercepts) we see that there two identical zeros are x = - 3 , and another two identical zeros at x = 2.
Thus the equation becomes:
f(x) = a( x + 3)(x + 3)(x - 2)(x - 2) or f(x) = a( x + 3)2(x - 2)2
To determine the value of a, substitute in the coordinates of the point (1 , - 8) which is on the graph:
- 8 = a(1 + 3)(1 + 3)(1 - 2)(1 - 2)
- 8 = 16a
a = - ![]()
The function notation for the graph is thus: f(x) = - ![]() ( x + 3)2(x - 2)2
( x + 3)2(x - 2)2
Example 3
Write the function notation for the graph shown below.
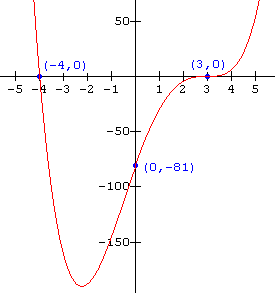
Solution
Since the graph is a quartic, its function may be written as:
f(x) = a(x - h)(x - k)(x - j)(x - m)
From the graph (the x-intercepts) we see that there three identical zeros are x = 3 , and another zero at x = - 4.
Thus the equation becomes:
f(x) = a( x + 4)(x - 3)(x - 3)(x - 3) or f(x) = a( x + 4)(x - 3)3
To determine the value of a, substitute in the coordinates of the point (0 , - 81) which is on the graph:
- 81 = a(0 + 4)(0 - 3)(0 - 3)(0 - 3)
- 81 = - 108a
a = ![]()
The function notation for the graph is thus: f(x) = ![]() ( x + 4)(x - 3)3
( x + 4)(x - 3)3
Note: The functions in the examples above each had four real roots. We seen in the previous lessons that it is possible for a quartic to have two or four complex roots and hence its graph will only have two x-intercepts or not have any x-intercepts at all. We will not be determining the function notation for this type of function in this course. The graphs below show examples of these types of quartic functions and are given for reference only.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
For each of the graphs below:
(a) Identify the type of function it represents (i.e. constant, linear, quadratic, etc.).
(b) Tell if the leading coefficient of the function is positive or negative.
(c) Indicate the number of real zeros and if they are distinct or identical.
1.  2.
2. 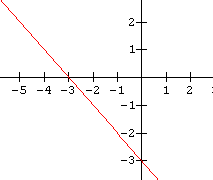
3. 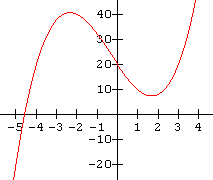 4.
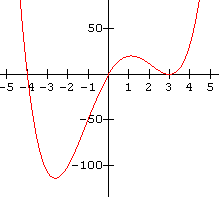
4. 
5. 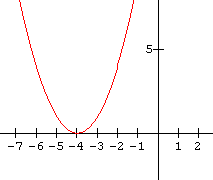 6.
6. 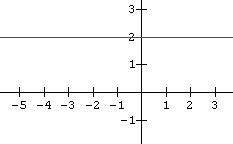
7. 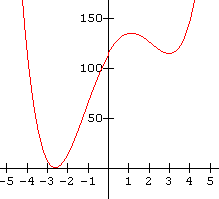 8.
8. 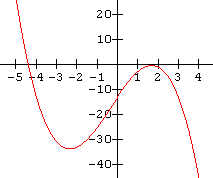
9. 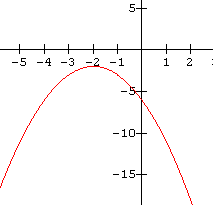 10.
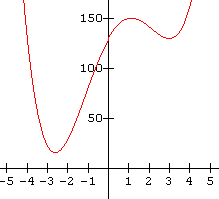
10. 
Find the function for each of the graphs shown below:
11.  12.
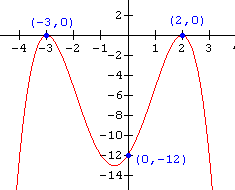
12. 
13. 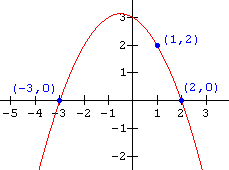 14.
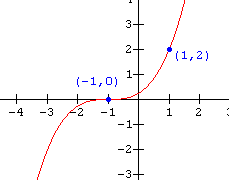
14. 
15. 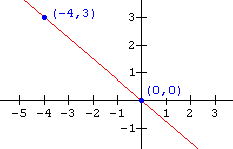 16.
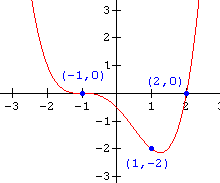
16. 
17. 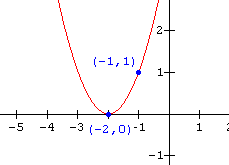 18.
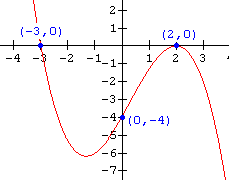
18. 
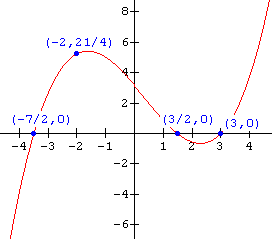
19. 
20. 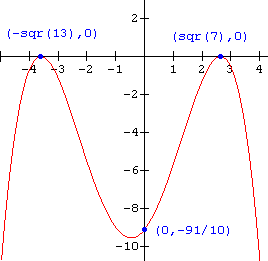 Note: sqr (13) means
Note: sqr (13) means ![]()
Test Yourself
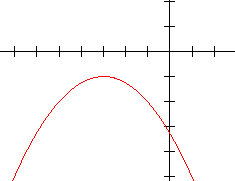
For each of the graphs below:
(a) Identify the type of function it represents (i.e. constant, linear, quadratic, etc.).
(b) Tell if the leading coefficient of the function is positive or negative.
(c) Indicate the number of real zeros and if they are distinct or identical.
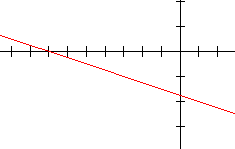
1. 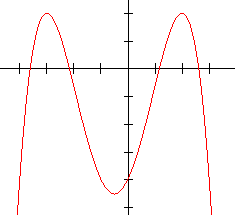 2.
2. 
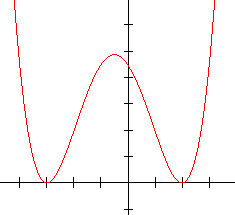
3. 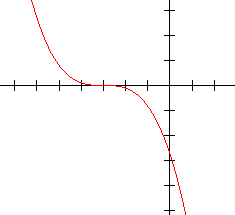 4.
4. 
5. 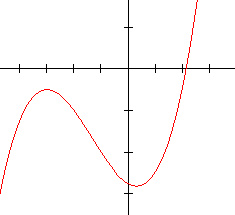 6.
6. 
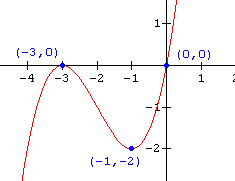
Find the function for each of the graphs shown below.
7. 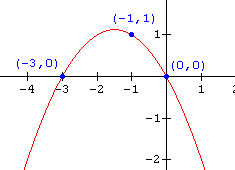 8.
8. 
9. 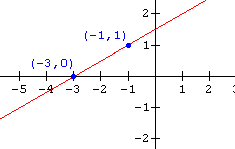 10.
10.