
Learning Resources
Lesson
Cubic Functions
Cubic functions have degree three. Examples of cubic functions are: f(x) = 2x3 + 3x2 - x + 1,
y = - 3x3 , g(x) = (x - 2)(x + 3)(x - 1) , p(x) = (x - 5)3 .
The "basic shape" of a cubic function can be likened to a line with a kink in it. If the leading coefficient is positive, it slopes upward to the right. This comparison is shown in the sketches below.
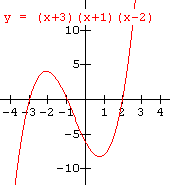
If the leading coefficient is negative, the graph slopes downward to the right as shown in the sketches below.
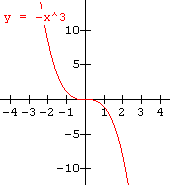
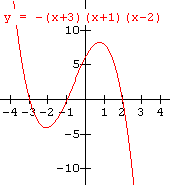
To draw the graph of a cubic function, we will use the same technique that we used for linear and quadratic functions in the last lesson. The "basic shape" of the graph of a cubic function may not be apparent from the few sketches shown above, but after we sketch a few the shape will become more obvious.
We will first consider a cubic polynomial that has three real roots and develop our understanding of the general graph from there.
Example 1
Use the zeros of the function to help sketch the graph of f(x) = (x + 4)(x + 1)(x - 2)
Solution
More examples of graphing cubic functions are contained on Page 2 of this lesson.
Cubic Functions (continued)
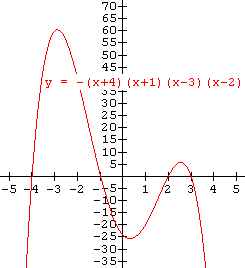
In Example 1 on Page 1 the leading coefficient was positive and the graph sloped upward to the right. We will now consider the function obtained by making the leading coefficient negative in that same expression. Notice that its graph slopes downward to the right.
Example 1
Use the zeros of the function to help sketch the graph of f(x) = - (x + 4)(x + 1)(x - 2)
Solution
Follow the exact same steps as is shown in Example 1 on Page 1. The graph below was found by finding the zeros and plotting them on the axes. Then a point was found in each of the regions determined by the zeros and they were plotted on the graph. Then a "smooth curve" was sketched through the points (note: do not simply connect the points with straight lines).
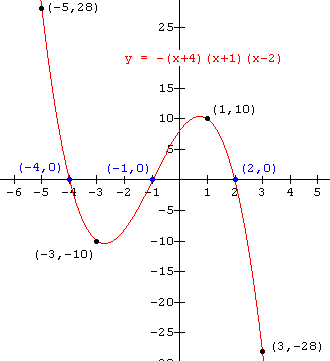
Notice in the graph that the points (- 3 , - 10) and (3 , 10) are not the lowest or highest points in their respective regions. It would be nice if we could locate these points, that is the local maxima and minima of the curve in these regions, but that is beyond the scope of this course. To find them you need an understanding of some of the concepts of calculus.
Recall: A local maximum is the largest value of the function in a particular region and a local minimum is the smallest value of the function in a particular region. For example, on the graph above there is a maximum value for f(x) in the region between -1 < x < 2 which is not the maximum value of the function since f(x) can be much larger in the region x < - 4.
Also note that unlike the quadratic function, the local maxima and minima of a cubic does not occur exactly halfway between the zeros. Thus the accuracy of the sketch (viz. the local maxima and minima) will be only an approximation based on our knowledge of the "basic shape" of the graph.
Both examples we have discussed so far had three distinct real zeros. All cubic functions with three distinct real zeros have that same "basic shape". The only difference will be where they cut the x-axis, i.e. their zeros, and where the maximum and minimum points within the regions are located.
We now want to look at a cubic function which has two identical roots, also called a double real root.
Example 2
Use the zeros of the function to help sketch the graph of f(x) = (x - 3)(x + 2)2
Solution
The next possibility we wish to explore is when a cubic has three identical real roots. This graph and a summary of our work on cubic polynomials is on Page 3 of this lesson.
Cubic Functions (continued)
We learned in our work on solving polynomial equations by factoring that a cubic polynomial equation could have three identical roots. Example 1 below shows the graph of such a polynomial.
Example 1
Use the zeros of the function to help sketch the graph of f(x) = - (x - 2)3 .
Solution
Notice that the leading coefficient is negative, which means the graph travels or slants downward to the right.
There is only one x-intercept, viz. (2 , 0) corresponding to the triple root x = 2. Mark it on the axis.
Pick a sample point either side of the zero and use it to help sketch the curve. Let us use x = 0 and x = 4. This gives f(0) = 8 and f(4) = - 8 . The final result is shown below.
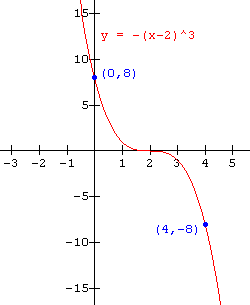
Note the "flattened" portion of the graph around the triple zero. Consider why this is happening. As x-values closer and closer to the zero are used (distance < | 1 | ), the difference between that x-value and the zero is very small. Since the y-value is the cube of that very small difference, the result will be an even smaller number. On the other hand, if the distance > | 1 |, the cube of that result increases more rapidly as we move away from the zero. To see this for yourself find f(1.7) and f(1.8) and note the difference between them. Then find f(4.7) and (4.8) and note the difference between them.
All of the examples we have discussed so far have had three real zeros. Sometimes there were two identical zeros and sometimes three identical zeros. However, it is possible that a cubic function would have only one real zero and the other two could be complex. We saw this when solving equations using factoring in earlier lessons in this unit. To see the significance of this on the graph, click [show] below.
Quartic Functions
Quartic functions have degree four. Examples of quartic functions are: f(x) = 2x4 + 3x3 - x + 1,
y = - 3x4 , g(x) = (x - 2)(x + 3)(x - 1)(x + 5) , p(x) = (x - 3)4 .
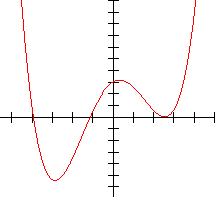
The "basic shape" of a quartic function can be likened to the shape of a "w". If the leading coefficient is positive, the "w" opens upward, if it is negative the "w" opens downward. This comparison is shown in the sketches below.
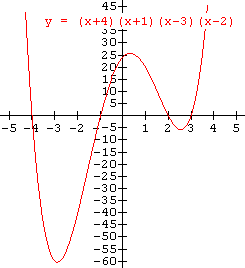
If we move these graphs up or down on the axes, we can see some of the relations between the zeros of the function and the x-intercepts of the graph.
Two identical plus two distinct real zeros. Only two distinct real zeros
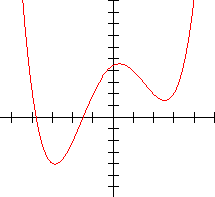
Only two identical real zeros No real zeros
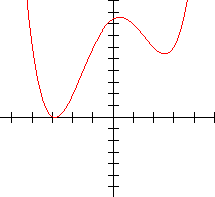
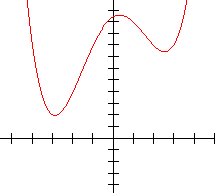
One distinct and three identical real zeros Four identical real zeros
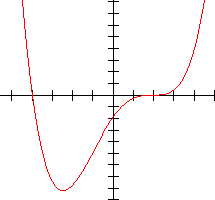
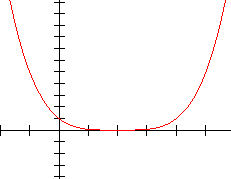
We will now use the zeros of the function and our idea of the "basic shape" to sketch the graph of a few quartic functions. This is done on Page 5 of this lesson.
Quartic Functions (continued)
Example 1
Use the zeros of the function to help sketch the graph of f(x) = (x + 4)(x + 1)(x - 2)(x - 3)
Solution
Example 2
Use the zeros of the function to help sketch the graph of f(x) = -(x + 4)(x + 1)(x - 2)2
Solution
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Use the zeros of the function and your knowledge of its "basic shape" to sketch the the graphs of the following functions.
1. f(x) = ![]() x(x + 3)(x - 2) 2. f(x) = -(x + 1)(x + 3)2
x(x + 3)(x - 2) 2. f(x) = -(x + 1)(x + 3)2
3. f(x) = x3 +4x2 - 4x - 16 4. f(x) = ![]() x(x + 4)( x + 2)(x - 3)
x(x + 4)( x + 2)(x - 3)
5. f(x) = - (x - 2)2(x + 3)2 6. f(x) = x4 -25x2 + 144![]()
7. f(x) = (x - ![]() )(x +
)(x + ![]() )(x +
)(x + ![]() ) 8. f(x) = ( x + 4)(x2 - 2)
) 8. f(x) = ( x + 4)(x2 - 2)
Test Yourself
Use the zeros and your knowledge of "basic shapes" to sketch the graphs of the following functions.
1. f(x) = - ![]() x(x - 2)(x + 2) 2. f(x) = x3 - 5x2 - x + 5
x(x - 2)(x + 2) 2. f(x) = x3 - 5x2 - x + 5
3. f(x) = - ![]() x(x - 3)3 4. f(x) x4 - 2x2 + 1
x(x - 3)3 4. f(x) x4 - 2x2 + 1