Learning Resources
Lesson
Constant Functions
You met the constant function in earlier mathematics courses. It is so named because it retains the same or constant range value no matter what the domain value becomes. Examples of the constant function are f(x) = 4 , g(x) = - 7 , y = 
, y = 
.
The general form of the constant function is: f(x) = k where k Î R .
You can graph the constant function f(x) = k by using a table of values. When you do, the graph will always be a horizontal line with y-intercept (0 , k). The only time it will have x-intercepts is when k = 0, then it has infinitely many of them since it is the equation of the x-axis.
When k is any number other than zero, there is no value of x that will make the function equal to zero (i.e. it has no zeros). If k = 0, then any number in the domain returns a range value of zero and thus every number from the domain is a zero of the function.
Knowing the "basic shape" of the graph of a function helps considerably when drawing the graph of a particular function of that type. The basic shape of the constant function is a horizontal line. To construct the graph of any constant function we can simply draw a horizontal line through one point that satisfies the function. The point usually chosen is the y-intercept. This is shown in the example below.
Example 1
Graph the function f(x) = - 2
Solution
We recognize that this is a constant function (no variable term). The y-intercept can be found by finding the value of the function at x = 0. In this case we have f(0) = - 2 . Plot the point (0 , - 2) and draw a horizontal line through it. This gives the graph below.
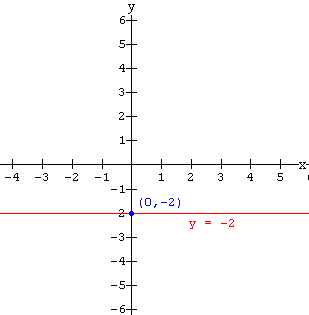
If you are not convinced that the graph of the constant function above is a horizontal line, consider some more points. For example: f(1) = - 2, which gives the point (1 , -2); f(2) = - 2, which gives the point (2 , - 2); f(- 5) = - 2, which gives the point (- 5 , - 2). Clearly these points all lie on a horizontal line since their y-coordinates are all the same.
Linear Functions
You have studied the graphs of linear functions in earlier grades. These functions are so named because their graphs are straight lines. Examples of linear functions are f(x) = 2x + 4 ,
f(x) = 
x - 5 , y = - 3x , 2x + 5y = 7.
The slope y-intercept form of the linear function is: f(x) = mx + b where m and b Î R .
Note that the degree of the linear function is one and it is referred to as a first degree function.
Note also that a constant function is a special case of a linear function in which the value of m, the coefficient of x, is zero.
In previous mathematics courses you studied the graph of linear functions by constructing a table of values and plotting the corresponding points. You also learned to graph linear functions using the slope and y-intercept.
However, in this lesson we will take a different look at these graphs. Remember the title of the unit we are doing is "Solving Polynomial Equations" so we want to connect the graph to the concepts of equation roots and function zeros. This is best understood by considering the following examples.
Example 1
Graph f(x) = 2x - 4
Solution
Quadratic Functions
Quadratic functions have degree two. Examples of quadratic functions are f(x) = 3x2 + 2x - 5 ,
g(x) = - 5x2 , y = x2 - 1. You may have studied these functions in earlier grades and know what the "basic shape" looks like. For those of you who may have forgotten this type of function, the graphs of the above examples are drawn below.
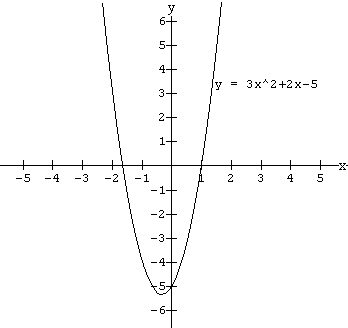
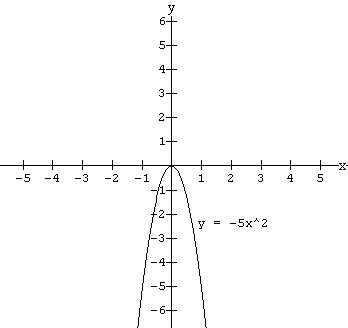
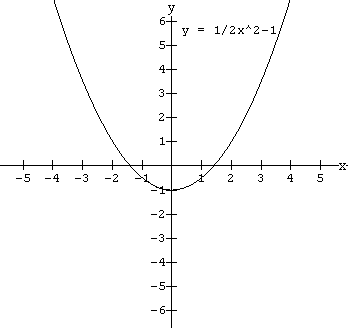
Note the "basic shape" is a u shaped curve. This curve is called a parabola and we will use this basic shape along with our knowledge of the zeros of a function to draw the graphs of quadratics.
There are many other different approaches to use to sketch the graph of a quadratic, some of which you may have used in previous mathematics courses. However, in this unit we are concerned with the "Roots of Polynomial Equations", which are the zeros of the corresponding quadratic function. Consequently, we will relate our graphs to these concepts.
Example 1
Use the zeros of the function and your knowledge of the "basic shape" to help sketch the graph of f(x) = x2 - 2x - 8
Solution
In the work we did in the previous section we discovered that a quadratic equation can have a double root, or the function a double zero. In terms of the graph, you should be able to visualize the two intercepts moving closer to each other until they finally become one point, indicating a double root. To see this happen click on the [show] button below.
The above graph could also have its "opening" downward. That is determined by the coefficient of the squared term. We will determine the direction of the opening by considering another point on the graph.
To graph quadratics that have a double root we can proceed much the same way as in the Example 1 above. There we looked at the zeros by factoring the quadratic. For example, we changed f(x) = x2 - 2x - 8 into f(x) = (x - 4)(x + 2). The factors immediately gave us the zeros and the y-intercepts of the graph. We then picked another point to determine the exact parabola required.
Example 2
Use the zeros of the function and your knowledge of the "basic shape" to help sketch the graph of f(x) = x2 - 6x + 9
Solution
Note that the function can be written as f(x) = (x - 3)(x - 3) or f(x) = (x - 3)2 . This indicates that the function has a double zero at x = 3. The only x-intercept is therefore (3 , 0). Plot this point and then evaluate the function at one other point to determine the placement of the rest of the basic parabolic shape.
Evaluate the function at x = 5, f(5) = 52 - 6(5) + 9 = 4 or using the other form f(5) = (5 - 3)2 = 4. Plot the point (5 , 4) and use it to sketch the rest of the graph as shown below.
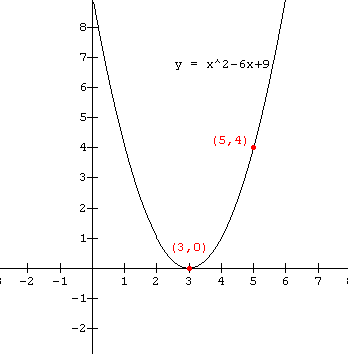
It should be obvious that if a quadratic function has no real zeros, its graph has no x-intercepts. This method cannot be used to sketch its graph because we cannot locate where the parabola is in the plane. The graphs below show some examples of quadratics that do not have real zeros. You should be able to use the skills from the last section to determine the complex roots of some of them.
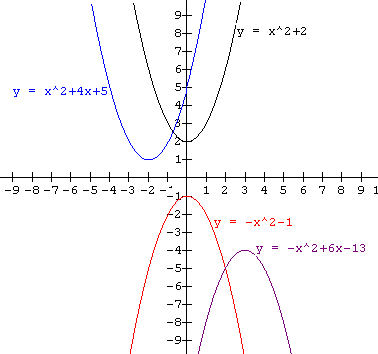
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Identify the real zeros (where they exist) and use your knowledge of its "basic shape" to help sketch the graph of each of the following functions. Do not use graphing technology other than as a check of your work.
1. f(x) = - 2 2. f(x) = 
3. f(x) = 2x 4. f(x) = - 
x + 1
5. f(x) = 3(x - 4) 6. f(x) = (x + 3)(x - 5)
7. f(x) = -(x + 1)2 8. f(x) = x2 - 10x + 21
9. f(x) = 6x2 + x - 5 10. f(x) = x2 - 4x + 8
Test Yourself
Identify the real zeros (where they exist) and use your knowledge of its "basic shape" to help sketch the graph of each of the following functions. Do not use graphing technology other than as a check of your work.
1. f(x) = 5 2. f(x) = 2(x + 3)
3. f(x) = 2x + 5 4. f(x) = 2(x - 1)(x + 4)
5. f(x) = - (x - 3)2 6. f(x) = 3x2 - 12
7. f(x) = x2 + 6x + 5 8. f(x) = 4x2 - 4x - 3