Learning Resources
Lesson
Division of Polynomials
Some of you may have learned in an earlier mathematics course how to apply the long division algorithm to polynomials. For those of you who may not have seen it before, or those who may need a review of the process and the terminology involved, the example below shows this algorithm in a step by step fashion.
Example 1
Divide using long division: (2x3 - 5x2 + x - 1) ¸ (x - 3)
Solution
The above long division algorithm can be time consuming. However, there is a way of shortening the process by using what is referred to as synthetic division. Example 2 below shows how the synthetic division algorithm is derived. Then in Example 3 the process is used instead of long division.
Example 2
Derive the synthetic division process using (2x3 - 5x2 + x - 1) ¸ (x - 3)
Solution
Example 3
Divide using synthetic division: ( 3x4 - 11x3 - 21x2 + 3x + 17 ) ¸ ( x - 5 )
Solution
Note: When using synthetic division some find it easier to use the negative of the constant in the divisor (in the example above use 5) and then add instead of subtract. That is more of a personal preference than a rule and is left to you to decide what you want to do.
Example 4
Find the quotient and remainder on dividing the polynomial - 5x3 + 14x - 7 by x + 2
Solution
The first thing to note is that there are powers of x missing from the dividend. That is because we generally do not write powers whose coefficients are zero. However, for division these coefficients must be included. Thus the coefficient arrays to use for the divisor and dividend are as shown below:
Note: You should have noticed that synthetic division only works when the divisor is of the form x - k, i.e. a linear polynomial with leading coefficient 1.
Note About Synthetic Division
It is important to note that synthetic division is only a means to an end. The end we want is to find the quotient when one polynomial is divided by another polynomial (viz. a linear polynomial). It is not necessary to use synthetic division since we can find this quotient using long division. However, once you know how to use it, synthetic division is much quicker. It is up to you if you want to use long division or synthetic division in the work that follows. Where division is necessary, this lesson will use synthetic division.
If you want to see more on synthetic division visit the site indicated by the URL below: http://www.purplemath.com/modules/synthdiv.htm
Remainder Theorem
The Remainder Theorem states that if a polynomial P(x) is divided by the linear polynomial x - k, the remainder is P(k).
No proof is offered for this theorem in this course, but we can test it with an example.
Example 1
If P(x) = x3 - 2x2 + 3x + 7 is divided by x - 2, is the remainder P(2)?
Solution
Dividing using synthetic or long division gives: Quotient = x2 + 3 and Remainder = 13 (the division is left to you to check)
P(2) = (2)3 - 2(2)2 + 3(2) + 7 = 8 - 8 + 6 + 7 = 13
Thus P(2) = remainder
This theorem can have a significant advantage when dealing with polynomials which have a high degree. For example, it would be virtually impossible using long division or synthetic division (there would be 98 terms with coefficients of zero) to find the remainder when P(x) = x100 - 1 is divided by x -1. However, it is very simple to find P(1).
Example 2
What is the remainder when P(X) = x4 - 2x2 - 7x + 6 is divided by x + 2 ?
Solution
Recall that the theorem describes division by x - k, thus we have to think of x + 2 as x - (- 2). This means the remainder is P(-2)
P(-2) = (-2)4 - 2(-2)2 - 7(-2) + 6 = 16 - 8 + 14 + 6 = 28
You may be asking what all this has to do with the roots of a polynomial equation. Well recall the following:
dividend = quotient x divisor + remainder
If the remainder is zero, then the quotient and divisor are both factors of the dividend. You already learned in the last lesson that if we can factor a polynomial we can find its roots. Thus the remainder theorem will be used to help us find factors of polynomials so that we can find their roots.
Example 3
Is x - 
a factor of 4x3 + 16x2 + 9x - 9 ?
Solution
There are two ways to determine this. One is to divide using synthetic or long division, the other is to use the remainder theorem and evaluate the polynomial for x = . The latter is used in this example. You should check it by using the division method.
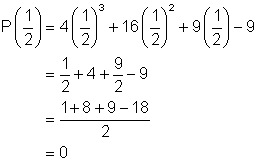
Using The Rational Roots Theorem
The necessity for this theorem is best shown by considering the examples from the Pre-test. The three examples there were to find the roots of each of the following equations:
x3 - 2x2 - 5x + 6 = 0 ; 12x3 + 20x2 - x - 6 = 0 ; x4 + x3 + 2x2 + 4x - 8 = 0
Up to this point factoring has been fairly easy. We could apply one of the patterns of
- common factors
- difference of squares
- trinomials
- grouping and removing a binomial common factor
However, none of these patterns seem to work on either of the equations above. Fortunately there is a theorem that we can use to help us to factor these polynomials. If is called the Rational Roots Theorem and it says:
Given the polynomial equation anxn + an - 1xn - 1 + ... + a1x + a0 = 0, then the rational number 
, expressed in lowest form, is a root of the equation if and only if p is a divisor of the constant term a0 and q is a divisor of the leading coefficient an .
As with the Remainder Theorem, no attempt is made in this course to prove this theorem. We simply take it and apply it to solving problems. In fact, this theorem is probably best understood by applying it to the examples above.
Example 1
Solve: x3 - 2x2 - 5x + 6 = 0
Solution
If we could "see" the factors immediately, that is how we would proceed. However, they are not readily apparent, so let us apply the Rational Roots Theorem.
The leading coefficient is 1. The only positive (q > 0) factor of 1 is 1. This is the value for q.
The constant term is 6. The factors of 6 are ± 1 , ± 2 , ± 3, ± 6. These are the values for p.
Thus, if there are any (and there may not be any) rational roots of this polynomial they have to come from the set 
.
Now comes the tedious work. There are two ways to determine which, if any, of these numbers is a root. One is to substitute each value into the polynomial to see if it works, i.e. makes the polynomial equal zero. The other is to use division, and divide the polynomial by each of the factors x - 6, x - 3, etc. to see if the remainder is zero (now you should see the advantage of synthetic division). We will do this problem by substitution:
P(-6) = (-6)3 - 2(-6)2 - 5(-6) + 6 = -252 , therefore - 6 is not a root.
P(-3) = (-3)3 - 2(-3)2 - 5(-3) + 6 = -24 , therefore - 3 is not a root.
P(-2) = (-2)3 - 2(-2)2 - 5(-2) + 6 = 0 , therefore -2 is a root.
Now we have a choice. We can continue substituting in the remaining possibilities, which in this case is not too bad because there are only a few of them.
The other possibility is to divide the original polynomial by the factor x + 2 ( remember x = -2 is the root, so x - 2 = 0, and this gives the factor x + 2), to get a polynomial of lower degree that we may be able to factor ( this new polynomial is called the depressed equation). We will use this latter approach so that you can see how it works and apply it to equations that have a multitude of possible rational roots.
We will use synthetic division: 2 | 1 - 2 - 5 6
2 - 8 6
1 -4 3 0
The quotient of the division is thus x2 - 4x + 3 . It is called the depressed equation and it gives the other factor of the polynomial. We can now rewrite the equation in factored form as follows:
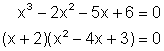
But the factor x2 - 4x + 3 is easily factored to (x - 3)(x - 1). We can thus write:
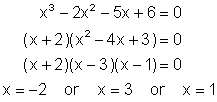
The above example looks more complicated than it really is because of all the commentary that was necessary to explain the process. The process can be summarized as follows:
Summary
- Use the Rational Roots Theorem to determine all the possible rational roots of the equation.
- Substitute or divide until you find one of the possibilities that actually is a root.
- Use this root and its corresponding factor to find the depressed equation.
- Solve the depressed equation using factoring if possible (or determine its possible rational roots and repeat the process).
Example 2
Find the roots of: x4 + x3 + 2x2 + 4x - 8 = 0
Solution
Factors of leading coefficient = 1
Factors of constant term = ± 1 , ± 2 , ± 4, ± 8
Possible rational roots = { - 8 , - 4 , - 2 , - 1 , 1 , 2 , 4 , 8 }
P(-8) = (-8)4 + (-8)3 + 2(-8)2 + 4(-8) - 8 = 3672 , therefore -8 is not a root.
P(-4) = (-4)4 + (-4)3 + 2(-4)2 + 4(-4) - 8 = 200 , therefore -4 is not a root.
P(-2) = (-2)4 + (-2)3 + 2(-2)2 + 4(-2) - 8 = 0 , therefore -2 is a root and x + 2 is a factor.
Use the factor x + 2 and division to find the depressed equation. We will use synthetic division:
2 | 1 1 2 4 - 8
2 - 2 8 -8
1 -1 4 - 4 0
We now have the coefficients and constant term of the depressed equation. Thus we can write the depressed equation as x3 - x2 + 4x - 4 = 0. But this is solvable using grouping and factoring.
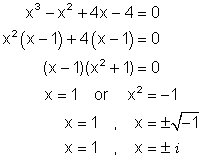
The solutions to the original equation x4 + x3 + 2x2 + 4x - 8 = 0 are thus { - 2 , 1, i , - i }
Note: In the examples we have done, the depressed equation has always been factorable over the set of rational numbers. That may not always happen. For example, you could end up with a quadratic equation that has complex roots ( remember our work in Lesson 2 of Section 1?). When that happens, we can still solve the depressed equation using the Quadratic Formula. However, some of you may not have covered that topic yet in your other mathematics courses, so we will avoid that type of example for the most part.
The following example includes such a polynomial just to show you how you can use the quadratic formula with the rational roots theorem to solve more difficult equations.
Example 3
Find the roots of the equation: 2x3 - 9x2 + 30x - 13 = 0
Solution
Factors of the leading coefficient = 1 , 2
Factors of the constant term = ± 1 , ± 13
Possible rational zeros are thus: 
P(-13) = 2(-13)3 - 9(-13)2 + 30(-13) - 13 = - 6318
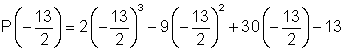= - 1138
P(-1) = 2(-1)3 - 9(-1)2 + 30(-1) - 13 = - 54
= 
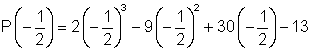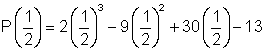= 0 Therefore, 
is a root and x - is a factor.
Now find the depressed equation:
- 1/2| 2 - 9 30 -13
- 1 4 -13
2 - 8 26 0
The depressed equation is thus 2x2 - 8x + 26 = 0 or x2 - 4x + 13 = 0 (removing common factor of 2). The problem is this equation doesn't factor over the set of real numbers. To solve it we need the quadratic formula which says that the solution to the equation ax2 + bx + c = 0 is:
Applying that to our depressed equation we get:
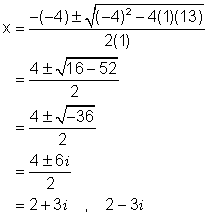
The solutions to the original equation 2x3 - 9x2 + 30x - 13 = 0 are thus { , 
, 
}
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
1. In each of the following, find the quotient and remainder on dividing the first polynomial by the second polynomial. Then express the first polynomial in the form:
(Divisor x Quotient) + Remainder.
(a) 4x3 - 5x2 + 3x - 2 by x + 1
(b) x4 - x2 + 1 by x + 1
(c) x3 + x2 - 4x - 4 by x - 2
2. (a) One of the factors of x3 + 5x2 + 8x + 4 is x + 1. Find the other factors.
(b) One of the factors of 6x3 - 35x2 + 47x - 12 is x - 4. Find the other factors.
3. Solve the following polynomial equations. If the depressed equation is a quadratic trinomial that does not have rational roots and you know how to use the quadratic formula, then find the other roots (irrational or complex) using it. Otherwise just find the rational roots.
(a) 6x3 - 5x2 - 8x + 3 = 0
(b) 10x3 + 19x2 - 5x - 6 = 0
(c) 3x3 + 5x2 + 4x - 2 = 0
(d) 2x4 + 5x3 + 15x2 + 45x - 27 = 0
Test Yourself
1. In each of the following, find the quotient and remainder on dividing the first polynomial A by the second polynomial B. Then express the first polynomial A in the form A = (Q x B) + R, with R = 0 or the degree of R less than the degree of B.
(a) 2x3 - 5x2 + x - 1 by x - 3 (b) 4x3 - 5x2 + 3x - 2 by x + 2
2. One of the factors of x3 + 2x2 - 4x - 8 is x - 2, find the other factors.
3. Solve the following polynomial equations:
(a) 6x3 - x2 - 12x - 5 = 0
(b) x4 + 4x3 + 6x2 + 4x + 1 = 0