
Learning Resources
Lesson
Roots of a Polynomial
We discussed the root of an equation in Lesson 01 of this section. There we said that a root of an equation is a number which when substituted for the variable makes the equation a true statement. The root of an equation is said to satisfy the equation or to be a solution of the equation. However, in that lesson we only discussed the roots of linear equations.
We now want to explore the roots of polynomial equations of degree four or less. To do this, consider the following:
Linear equation Root
x + 1 = 0 x = - 1
x - 4 = 0 x = 4
2x + 1 = 0 x = - ![]()
The principle of zero products tells us the product mn = 0 if and only if m = 0 or n = 0. Applying that to the above equations we have:
(x + 1)(x - 4)(2x + 1) = 0 or 2x3 - 5x2 - 11x - 4 = 0
Are the roots of the original linear equations also roots of the new trinomial formed from their product? To check, simply substitute into the trinomial:
2(- 1)3 - 5(- 1)2 - 11(-1) - 4 = - 2 - 5 +11 - 4 = 0 (therefore - 1 is a root)
2(4)3 - 5(4)2 - 11(4) - 4 = 128 - 80 - 44 - 4 = 0 (therefore 4 is a root)
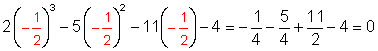 (therefore -
(therefore - ![]() is a root)
is a root)
Thus the roots of the trinomial are the roots of the linear factors from which the trinomial was obtained. Although this does not constitute a proof, it implies that the roots of a polynomial equation can be found by finding its linear factors. This is in fact true, and it suggests the following method of solving polynomial equations and is obtained by reversing the above process.
- Rearrange the polynomial equation so that it is equal to zero.
- Factor the polynomial into its linear factors.
- Apply the principle of zero products and solve each linear equation associated with each of the factors.
- Check your solution by substituting into the original equation.
Example 1
What are the roots of (x - 5)(x + 3)(2x - 1) = 0 ?
Solution
By the principle of zero products: x - 5 = 0 so 5 is a root; x + 3 = 0 so - 3 is a root; 2x - 1 = 0 so ![]() is a root. Thus the roots = { - 3 ,
is a root. Thus the roots = { - 3 , ![]() , 5 }
, 5 }
Note 1: If a polynomial in x does not have a constant term, then one of its factors must be x. Using the above reasoning, this gives x = 0 as one of the linear equations, and thus 0 is a root of the original polynomial.
Note 2: Since the degree of an equation determines how many linear factors it can have, e.g. degree 2 has 2 factors, degree 3 has 3 factors, etc., and for each linear factor there is a root, it implies the number of roots of a polynomial equation is determined by its degree. This is only the case if we count a double root twice, e.g. (x - 3)2 = 0 has two identical roots of 3.
Of course the polynomial in Example 1 above is already factored for you. In the examples on the following pages the polynomials are not in factored form. To see more about how to solve them go to the next page of this lesson.
Complex Roots
Sometimes it is not possible to factor a polynomial using the real number system. However, if complex numbers are used the polynomial becomes factorable. Consider the following, the first is a difference of squares that can be factored using real numbers. The second is a sum of squares that cannot be factored using real numbers but can be converted to a difference of squares by introducing the imaginary number i (recall that i 2 is equal to - 1).
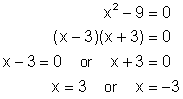
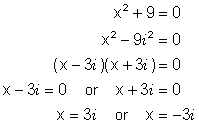
Both of the above equations can be solved without factoring if we recall the concept of square root. Before we look at how to do that, recall that the symbol ![]() stands for only the principal square root. To show both square roots of a number we have to indicate both the principal or positive square root and the negative square root. This is indicated symbolically as
stands for only the principal square root. To show both square roots of a number we have to indicate both the principal or positive square root and the negative square root. This is indicated symbolically as ![]() .
.
If we look again at the examples above and apply this method we get the following:
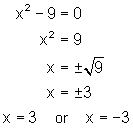
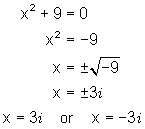
Note: This method of solving quadratic or second degree equations using the square root property only works when there is no linear term.
It is entirely up to you which method you use to solve quadratics without a linear term (factoring or the square root property). In either case, the imaginary number roots will be found if they exist.
You will also find other quadratic polynomials (e.g. x2 + x - 11 = 0 ) that cannot be solved by factoring even though some of them may have real roots. To overcome this we use the quadratic formula that you may recall from your work in a previous mathematics course. However, the examples in this lesson are chosen so that you will not encounter this situation. We will come back to this in a later lesson.
Finding Roots
The technique of finding the roots of a polynomial equation using factoring is summarized as follows:
- Rearrange the polynomial equation so that it is equal to zero.
- Factor the polynomial into its linear factors.
- Apply the principle of zero products and solve each linear equation associated with each of the factors.
- Check your solution by substituting into the original equation.
This process is best explained by the use of examples.
Example 1
Solve: x2 + 4x = 21
Solution
Example 2
Solve: x3 - 4x2 + 9x - 36 = 0
Solution
Example 3
Solve: x4 - 2x2 - 8 = 0
Solution
Compare Examples 2 and 3 above. In Example 2, factoring was used to get the imaginary root but in example 3 the square root property was used. You should do each of them again using the opposite method to what was used in the example.
Example 4
Solve: 4x(3x - 1) = 5(3x - 1)
Solution
The temptation with this example is to divide both sides by 3x - 1. But if you do that one of the solutions will be "lost". To solve any polynomial equation, unless you are using the square root property, you must first get everything on one side and let it equal to zero. Thus we have:
4x(3x - 1) - 5(3x - 1) = 0
You can one proceed in one of two ways. The straight forward was is to factor out the common binomial factor. However, if you did not see this you could multiply out, simplify, and then factor the resulting trinomial. It is a more round about way but still works. Both methods are shown in their completion below.
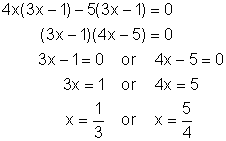
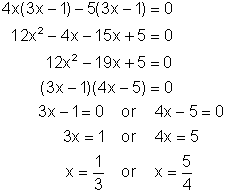
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Find all roots, real or imaginary, for each of the following equations:
1. 7x2 - 28x = 0 2. x2 - 5x + 6 = 0
3. x3 - 3x2 = 28x 4. x3 - 2x2 - 4x + 8 = 0
5. 3x2 = 2x + 8 6. x4 - 9 = 0
7. 2x2 + x = 6 8. 4x2 - 20x + 25 = 0
9. x2 - 6x - 16 = 0 10. 6x2 - 12x + 6 = 0
11. ![]() = 0 12. x4 - 3x2 + 2 = 0
= 0 12. x4 - 3x2 + 2 = 0
13. 12x4 - 5x2 - 2 = 0 14. 3x(2x + 5) = 2(2x + 5)
15. 2x3 + x2 - 6x = 3 16. x2(3x - 1) - 3x(3x - 1) + 2(3x - 1) = 0
Test Yourself
Find all roots, real or imaginary, for each of the following equations:
1. 3x2 - 7x = 0 2. 16x2 - 25 = 0
3. x2 - 10x = 24 4. 8x2 + 19x - 15 = 0
5. 2x3 - x2 + 2x - 1 = 0 6. 10x3 + 5x = 6x2 + 3
7. 2x4 + 7x2 = 15 8. 4x(2x - 3) = 2(2x - 3)
9. 2x3 + 2x2 - 24x = 0 10. 3x4 - 75 = 0