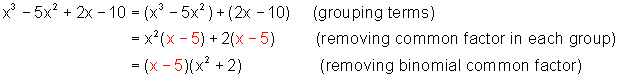Learning Resources
Lesson
Common Factors
Your ability to factor successfully is directly linked to your ability to multiply. If you have difficulty multiplying polynomials you should review that topic before you continue with this lesson.
Removing a common factor is a matter of finding the greatest common factor of each of the terms of the polynomial and then applying the distributive property in reverse. This is illustrated in the examples below.
Example 1
Factor completely: 12x - 8
Solution
The greatest common factor of the two terms is 4. We can rewrite the polynomial so that each term is a product of 4 and some other factor. We then apply the distributive property in reverse.
12x - 8 = 4(3x) - 4(2) = 4(3x - 2)
Example 2
Factor completely: x(y + 2) - 3(y + 2)
Solution
In this example the common factor is already written. The only difference is that it is a binomial term.
x(y + 2) - 3(y + 2) = x(y + 2) - 3(y + 2) = (y + 2)(x - 3)
Example 3
Factor completely: x3 - 5x2 + 2x - 10
Solution
In this example there is no factor common to all four terms of the polynomial. However, if the terms are grouped, a binomial factor emerges.
Example 4
Factor completely: ![]()
Solution
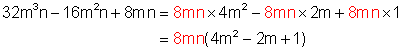
Difference of Squares
As noted on page 1 of this lesson, your ability to factor is linked to your ability to multiply. In fact, factoring is the reverse process of multiplication. To understand the pattern for factoring the difference of squares, first consider the following multiplications.
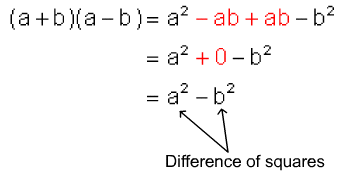
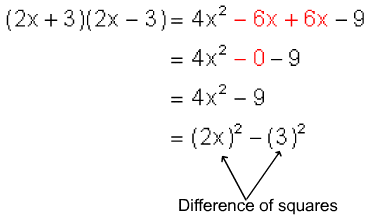
Notice the products in both cases are a difference of squares. Now look closely at the factors that were multiplied to get these products. In both cases the factors used were the sum of the two numbers and the difference of the two numbers. We will use this pattern to factor differences of squares. The pattern can be summarized as follows:
![]()
This factoring pattern is shown in the following examples.
Example 1
Factor completely: 64 - x2
Solution
64 - x2 = 82 - x2 = (8 - x)(8 + x)
Example 2
Factor completely: ![]()
Solution
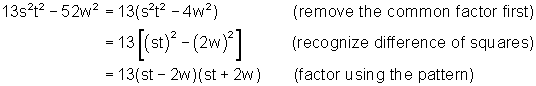
Example 3
Factor completely: ![]()
Solution
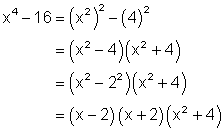
All of the above examples factored over the set of integers that we discussed in Unit 1 of this course. It is also possible to factor the difference of squares using other sets of real numbers, and in particular it is often beneficial to use the set of radicals as shown below.
Example 4
Factor completely over the set of real numbers: ![]()
Solution
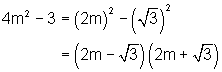
Sometimes each of the terms of a polynomial are themselves binomial terms. The basic pattern of the first term minus the second times the first term plus the second does not change. This is shown in the following example.
Example 5
Factor completely: ![]()
Solution
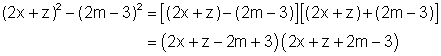
Trinomials of form x2 +bx + c
This part of the lesson looks at trinomials where the leading coefficient is 1. That is, trinomials of the form x2 + bx + c. You will probably recall using algebra tiles in earlier grades to help you factor these expressions. Algebra tiles are a good aid to understanding, but they are not an efficient process to use.
You now need to be able to factor mentally by considering a pattern. That pattern can only be seen if you can multiply efficiently. As noted in earlier pages in this lesson, the key to factoring is your ability to multiply.
To see the pattern necessary to factor trinomials of this type, consider the following multiplication.
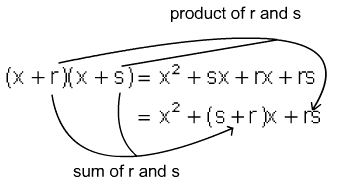
Thus a trinomial x2 + bx + c can be factored if we can find two numbers whose product is c (the constant term) and whose sum is b (the coefficient of the linear term). The two numbers may both be positive, both be negative, or one may be positive and the other negative. Study the examples below to help you apply this pattern to factoring these polynomials.
Example 1
Factor completely: x2 + 15x + 54
Solution
As a check, multiply the factors above to be sure you get x2 + 15x + 54. If you can multiply you should never have factors that are incorrect. You may not be able to find them, but once you have them, if you check by multiplying you will always know if they are correct.
Example 2
Factor completely: x2 - 14x + 40
Solution
As a check, multiply the factors to be sure you get x2 - 14x + 40. In the above examples, all the factors are shown for the sake of demonstration. When you are factoring, once you have the desired numbers you are finished. If you can "see" the required numbers quickly, the factoring becomes fairly easy.
Example 3
Factor completely: x2 - 6x - 72
Solution
Of course we can combine this type of factoring with the other types we have learned, especially the common factors. In fact, whenever you are factoring, always look to see if there are any common factors, and if there are remove them first. This is shown in the example below.
Example 4
Factor completely: 5x2 + 20x + 15
Solution
First remove the common factor 5 : 5x2 + 20x + 15 = 5(x2 + 4x + 3)
To factor the remaining trinomial, we need two factors whose product is 3 and whose sum is 4. These are obviously 1 and 3. Thus the factors are:
5x2 + 20x + 15 = 5(x + 3)(x + 1)
Example 5
Factor completely: x2 - 14x + 49
Solution
We need two factors whose sum is -14 and whose product is 49. This gives:
x2 - 14x + 49 = (x - 7)(x - 7)
Because the two factors are the same we may write x2 - 14x + 49 = (x - 7)2 . When the factors of a trinomial can be written as one factor squared, we say that the trinomial is a perfect square trinomial.
Trinomials of the type ax2 + bx + c
When the coefficient of the squared term is a number other than one, it is sometimes difficult to "see" the factors required to give the appropriate sums and products. One method used to overcome this is to "decompose" the trinomial and use grouping and the skill of common factors. This is shown in the following example.
Example 1
Factor completely: 8x2 + 10x + 3
Solution
Example 2
Factor completely: 2x2 - 7x - 15
Solution
As noted on the previous page of this lesson, you should always remove any common factors as a first step. This is shown in the following example.
Example 3
Factor completely: 6x3 - 15x2 - 36x
Solution
Example 4
Factor completely: 4x4 - 13x2 - 9
Solution
The trinomial in this example has the basic pattern of a quadratic, viz. ax2 + bx + c, however it is to degree 4 instead of the usual degree 2. Simply recall that x4 is (x2)2 and the method becomes exactly the same. Check for common factors and, if none exist (as they don't in this case), proceed to apply the above technique.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Factor completely the polynomials in exercises 1 - 20 over the system of real numbers.
1. 15xy - 10xy2 2. 18a5 - 27a4 3. x(a + b) + y(a + b)
4. 2ax - 3bx - 2ay + 3by 5. x2 - 9x + 20 6. 25 - 10x + x2
7. x2 + 4x - 21 8. 50a2 + 20ab + 2b2 9. 2x2 + 3x + 1
10. 6x2 - 11x - 10 11. 6x2 - 13x + 6 12. 2x2 + 5x - 12
13. 10x2 - 640 14. 2x2y2 - 8 15. x2 - (y - h)2
16. ![]() 17. 8x3 + 4x2 - 2x - 1 18. 4x2 - 32x + 64
17. 8x3 + 4x2 - 2x - 1 18. 4x2 - 32x + 64
19. x4 - 13x2 + 36 20. -6x2 - 16x - 10
21. The surface area of a right circular cylinder is given by the formula ![]() . Rewrite the formula with the right hand side in factored form.
. Rewrite the formula with the right hand side in factored form.
Test Yourself
Factor completely each of the following polynomials over the real number system.
1. 3x2 + 6x - 12 2. 5x2 - 45 3. 112 - 7x2
4. x4 - 25 5. x2 - 7 6. n2 - 16n + 64
7. 2x2 + 14x + 12 8. q2 - 13q + 12 9. s2 + 16s - 36
10. 5y2 + 13y - 6 11. 6p2 - 17p + 12 12. 12x2 + 21x + 9
13. 49m2 - 16 14. ![]() 15. a3 + 3a2 - a - 3
15. a3 + 3a2 - a - 3