
Learning Resources
Lesson
Polynomials
Consider the following algebraic expressions which are collectively referred to as polynomials:
Expression Name Degree Leading coefficient Constant term
5x3 + 3x2 - 4 trinomial 3 5 - 4
12x11 - 2x9 binomial 11 12 none
![]() binomial 4
binomial 4 ![]() none
none
![]() trinomial 3
trinomial 3 ![]() none
none
Such expressions should not be new to you since you studied both linear and quadratic polynomials in earlier mathematics courses. The above examples suggest the following definition for polynomials.
Definition: A polynomial is an algebraic expression of the form
anxn + an - 1xn - 1 + ... + a1x + a0
where n is a non-negative integer, x is a variable, and an , an - 1, . . ., a1, a0 are real numbers.
The numbers an , an - 1, . . ., a1, a0 occurring in the polynomial are called coefficients. an is the coefficient of xn, an - 1 is the coefficient of xn - 1, and so on.
The number an is called the leading coefficient; it is the coefficient of the highest power of x occurring in the polynomial. The number a0 is called the constant term of the polynomial.
If an¹ 0, then n is called the degree of the polynomial. It is the value of the exponent of the highest power in the polynomial.
If n = 0 in the polynomial expression above, the polynomial has degree zero and consists of just one term, viz. a0. Such a polynomial is called a constant polynomial.
If n = 1 in the polynomial expression above, the polynomial has degree one and we have the expression a1x + a0 .This is called a linear polynomial.
If n = 2 in the polynomial expression above, the polynomial has degree two and we have the expression a2x2 + a1x + a0 . This is called a quadratic polynomial.
Similarly we can define a polynomial of degree three, which is called a cubic polynomial, and one of degree four which is called a quartic polynomial.
Examples
| 3x4 + 2x3 + x | Polynomial has degree four. It is called a quartic polynomial. It has no constant term and its leading coefficient is 3. |
| - 4x + 5x3 + 2x2 - 7 | Polynomial has degree three. It is called a cubic polynomial. Its constant term is - 7 and its leading coefficient is 5. |
| Polynomial has degree two. It is called a quadratic polynomial. Its leading coefficient is |
In this lesson we will only be concerned with linear polynomials. We will review how to find the root of an equation which contains a linear polynomial. We will also discuss the zero of a linear polynomial function and the x and y intercepts of its graph. This is done in the next pages of this lesson.
Finding the Root
A root of an equation is a number which, when substituted for the variable, makes the equation a true statement. The root of an equation is said to satisfy the equation or to be a solution of the equation. However, the term solution more often refers to the process of finding the root.
Example 1
4 is a root of the equation 3x - 7 = 5 because 3(4) - 7 = 12 - 7 = 5
- 2 is not a root of the equation 3x - 7 = 5 because 3(- 2) - 7 = - 6 - 7 = - 13 ¹ 5
We know how to verify if a given number is a root - we simply substitute it into the equation and see if it satisfies or makes the equation true. But what if the root is not given? How do we go about finding it? That is what is dealt with in this and subsequent lessons in this section.
The process of solving an equation (i.e. finding its roots) will be discussed for polynomial equations of degree four or less. This lesson deals only with equations of degree one, i.e. linear equations.
The technique of solving a first degree equation is to isolate the term containing the variable by using addition, subtraction, multiplication, and division. Just remember that you must balance the equation, i.e. what you do to the terms on one side of the equal sign you must do to the terms on the other. This is best explained by means of the examples below.
Example 2
Find the exact root of ![]()
Solution

Thus we can say that -1 is the root of the equation. We can verify this by substituting - 1 for x in the original equation. That is left for you to do.
Example 3
Find the exact root of ![]()
Solution
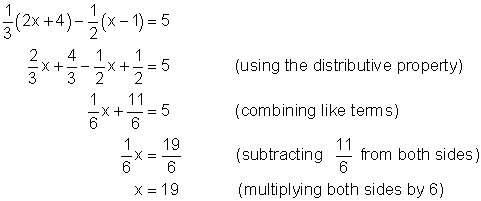
It is left to you to verify that 19 is the root by substituting it for x in the original equation.
Example 4
Find the exact root of ![]()
Solution

The root is verified below. Note that it is best to work with each side of the equation independently to see if the same answer results when the number is substituted for x.
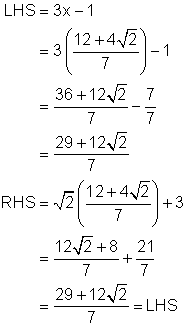
Zeros of Linear Functions
A zero of a function is the value of the argument (i.e. domain value) for which the value of the function (i.e. range value) is zero. This is shown in the diagram below:
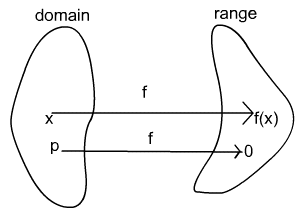
In the above diagram, p is a zero of the function f because f(p) = 0. Thus, to find the zero of a function you let the function equal zero and solve the resulting equation in the usual method. This is shown in the examples below.
Example 1
Find the exact zero of the function ![]()
Solution
Let the function equal zero and solve the resulting equation:
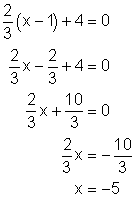
Example 2
Find the exact zero of the function ![]()
Solution
Let the function equal zero and solve the resulting equation:
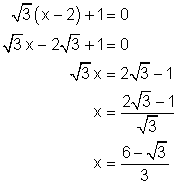
The zeros in both examples can be verified by substituting them into the original function to see if they return a value of zero.
Intercepts
When a graph is drawn in the coordinate plane it may cut across the x-axis or y-axis or both. If it does, the point where it cuts or crosses is referred to as the intercept.
The point on the x-axis is the x-intercept and the point on the y-axis is the y-intercept. This is shown in the graph below.
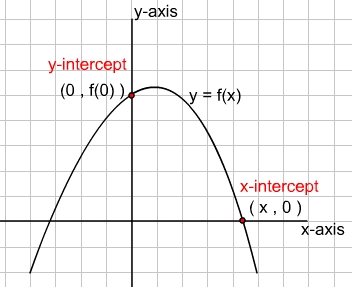
The same terminology is used regardless of the type of graph. As you know from previous mathematics courses, the graph of a linear or first degree polynomial is always a straight line. Nevertheless, the concept of the intercepts is the same.
To find the x-intercept of the graph of any equation we let the y or f(x) value equal zero and solve the resulting equation for x. This is shown in the example below:
Example 1
Find the x-intercept of the graph of the function ![]()
Solution
The y or f(x) coordinate of the x-intercept point is zero, so substitute this into the function:
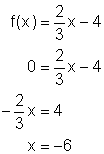
The x-intercept is 6. The coordinates of the point are thus (-6 , 0)
To find the y-intercept of the graph of any equation we let the x value equal zero and solve the resulting equation for y or f(x). This is shown in the example below:
Example 2
Find the y-intercept of the graph of the equation ![]()
Solution
The x coordinate of the y-intercept point is zero, so substitute this into the equation:
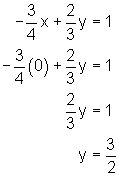
The y-intercept is ![]() . The coordinates of the point are thus (0 ,
. The coordinates of the point are thus (0 , ![]() )
)
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
1. Given the polynomial 2x2 - 4x3 + 7 - 5x , identify the following:
(a) the type of polynomial (i.e. linear, quadratic, etc.)
(b) the leading coefficient.
(c) the constant term.
(d) the degree of the polynomial.
2. Find the exact root of each of the following:
(a) 4x - 7 = 5 (b) ![]()
(c) 3(2x - 1) + 5x = 2 (d) ![]()
(e) ![]() (f) -4.2x - 2x = - x + 10.4
(f) -4.2x - 2x = - x + 10.4
(g) ![]() (h)
(h) ![]()
(i) 4(x - 2) - 9 = 2x + 7 - 3x + 12x (j) ![]()
3. Find the exact zeros of the following linear functions:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]()
4. Find the exact x and y intercepts of the graphs of the following:
(a) 2x - 3y = 1 (b) ![]()
Test Yourself
1. Given the polynomial 4 - 3x + 2x2 - 7x3 + x4 , identify the following:
(a) the type of polynomial (i.e. linear, quadratic, etc.)
(b) the leading coefficient.
(c) the constant term.
(d) the degree of the polynomial.
2. Find the exact root of each of the following:
(a) ![]() (b)
(b) ![]()
(c) ![]() (d) 2.3(1.2x - 4.5) - 3.1(x - 0.2)= - 11.43
(d) 2.3(1.2x - 4.5) - 3.1(x - 0.2)= - 11.43
(e) ![]() (f)
(f) ![]()
3. Find the exact zero of the following linear function: ![]()
4. Find the x and y intercepts of the graph of the function: ![]()