Learning Resources
Lesson
Defining Pure Imaginary Numbers
The imaginary number system was developed in response to problems that could not be answered using the real numbers. For example, there is no real number answer to the question "Which number squared gives -1?". Mathematically this same question can be stated as:
Solve for x: x2 = - 1 or x2 + 1 = 0
In order to solve equations similar to this, a new number system had to be developed. The basis for this number system would be the number which when squared gives the answer -1. The problem mathematicians had was what symbol to use to represent this new number. Mathematicians finally designated this new number with the symbol i and it had the property:
Definition: i 2 = -1
Note: It was the famous eighteenth-century Swiss mathematician Euler (pronounced Oiler) that introduced the symbol i . It is possible that he may have chosen i because it is the first letter of the Latin word imaginarius (imaginary).
From the above definition we can also write that 
, and this can be used along with the above definition to simplify expressions containing these numbers. This is shown in the following examples:
Example 1
Note: The i is generally written last when it is combined with an integer, i.e. we write 5i not
i 5 .
Example 2
Note: The i is generally written first when it is combined with a radical, i.e. we write 
not 
. The main reason for this is to avoid confusion caused by sloppy notation which shows 
as 
.
Example 3
Note: The i is placed after the integer but before the radical.
The above examples lead us to the following definition for pure imaginary number:
Definition: A pure imaginary number is any number of the form bi , where b is real and 
.
This term pure is used to distinguish these numbers from numbers which have a real part as well as an imaginary part and which are written in the form a + bi . These numbers are called complex numbers and will be discussed in the next lesson.
Operations Using Pure Imaginary Numbers
We can add, subtract, multiply and divide pure imaginary numbers using the rules previously developed for real numbers and the principles of algebra. For example, addition and subtraction of imaginary numbers is defined as follows:
Definition: If a and b are real numbers, then ai + bi = (a + b)i
Example 1
Similarly, applying what we know about real numbers and algebra, we define multiplication as follows:
Definition: If a and b are real numbers, then a(bi) = abi and (ai)(bi) = abi 2 = - ab
You have to be very careful when multiplying pure imaginary numbers. You must apply the definition before you multiply, otherwise you will get an incorrect answer. This is shown below:
correct: 
incorrect: 
Applications of the above definitions are shown in the following examples:
Example 2
When raising an i -number to a power you will always be involved with raising -1 to a power, the result of which is always 1 or -1. This leads to an interesting conclusion that is suggested by the four different powers shown in the following example.
Example 3
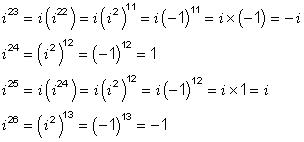
Continuing the above pattern, what would be the value of i 27 ?
Example 4
As Roots of Equations or Zeros of Functions
In previous courses you learned how to solve certain polynomial equations and we will deal more with that topic later in this unit. For now, recall that if a number is a root of an equation, it makes the equation true when substituted in place of the variable. Similarly a number is a zero of a function if it makes the value of the function equal to zero when it is substituted for the variable. Mathematically we say this as follows:
a is a zero of the function f(x) if and only if f(a) = 0
This is shown in the following examples.
Example 1
Show that 
is a root of the equation x2 + 12 = 0
Solution
Substitute for x in the left hand side of the equation and see if it works out to be the same as the right hand side, i.e. see if it makes the equation true.
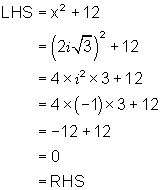
Thus we know that is a root of the equation x2 + 12 = 0.
Example 2
Show that 5i is a zero of the function f(x) = x3 + 2x2 +25x + 50
Solution
Substitute 5i into the function for x and see if the answer works out to be zero.
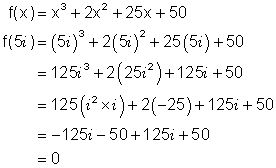
Thus 5i is a zero of the function (i.e. makes the function equal to zero)
We will return to the zeros of polynomial functions in another lesson in this unit. There we will work on ways of finding the zeros for any given polynomial function of degree 4 or less.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Write each of the following numbers as a pure imaginary number in the form bi and simplify.
1. 
2. 
3. 
4. 
Simplify each of the following:
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. Show that 
is one of the roots of the equation x3 - 3x2 + 2x = 6
17. Show that - 2i is one of the zeros of the function f(x) = x4 - 16
Test Yourself
Write each of the following numbers as a pure imaginary number in the form bi and simplify.
1. 
2. 
3. 
4. 
Simplify each of the following:
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. Show that 
is one of the zeros of the function x3 - 2x2 + 12x - 24