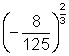Learning Resources
Lesson
Rational Exponents
We have already dealt with properties of integer exponents. Rational exponents should be defined in such a way that the properties of integer exponents will still apply. Consider the power of a power property, viz. (am)n = amn and see how it leads to a definition for rational exponents in terms of radicals.
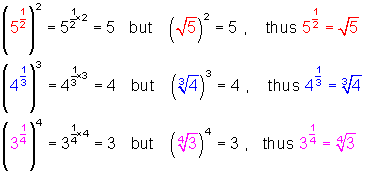
However, we have to be careful about applying the laws of integral exponents to rational exponents without thinking closely about them. Consider the following:

The above example implies that ![]() , and this we know is not true. The problem stems from the fact that we used a negative base, viz. -3, for the power. This led to taking the square root of a negative number, which we know is impossible in the real number system. Thus when we define rational exponents in general we have to specify that the base is a positive number.
, and this we know is not true. The problem stems from the fact that we used a negative base, viz. -3, for the power. This led to taking the square root of a negative number, which we know is impossible in the real number system. Thus when we define rational exponents in general we have to specify that the base is a positive number.
The above examples and discussion suggest the following:
Definition: If b is a positive real number and n is any positive integer greater than 1, then
![]()
For example: ![]()
We can now apply this definition along with what we already know about exponents and radicals to get a more comprehensive definition for rational exponents. Consider the following:

Note the relation of the fractional exponent to the radical. The numerator of the fraction is the exponent for the power and the denominator is the index of the radical. This leads to the following:
Definition: If b is a positive real number, n is any positive integer greater than 1, and m is any integer, then
![]()
Following are some examples of the application of this definition.
Example 1
Convert each of the following to the exponential form: ![]() ;
; ![]() ;
; ![]()
Solution
![]() ;
; ![]() ;
; 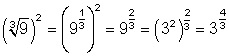
Example 2
Convert each of the following to simplest radical form: ![]() ;
; ![]()
Solution
![]() ;
; 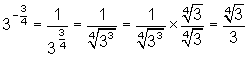
Example 3
Evaluate each of the following: 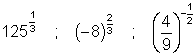
Solution
![]()
![]()
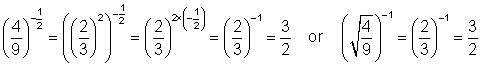
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
1. Rewrite using positive rational exponents. All variables denote positive numbers.
![]()
2. Rewrite each expression using radicals instead of fractional exponents. Simplify when
possible.
![]()
3. Evaluate each expression:
(a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]() ; (d)
; (d) ![]()
(e) 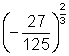 ; (f)
; (f) ![]() ; (g)
; (g) 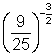 ; (h)
; (h) 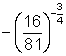
Test Yourself
Express each of the following as a power with a fractional exponent.
![]()
Express each of the following as a radical in simplest form:
5. n1.5 6. ![]()
Evaluate each of the following expressions. Leave each irrational answer in simplest radical form. Do not use a calculator.
7. ![]() 8.
8. 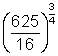 9.
9. ![]()
10. 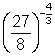 11.
11. ![]() 12.
12.