
Learning Resources
Lesson
Monomial Denominators
When simplifying expressions, if an expression contains a radical in a denominator, we rationalize the denominator. That is, we find an equivalent expression with no radicals in the denominator. To do this we multiply the expression by a form of the number 1 (hence the expressions are equivalent) that will make the denominator a rational expression, i.e. contains no radicals. This procedure is shown in the following examples where the denominators are monomial expressions.
Example 1
Simplify (i.e. rationalize the denominator) ![]()
Solution
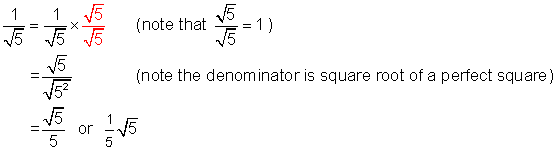
Example 2
Simplify: ![]()
Solution
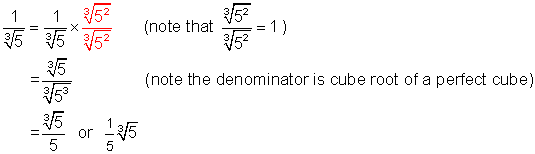
Example 3
Simplify: ![]()
Solution
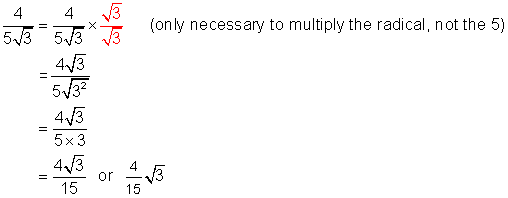
Example 4
Simplify: ![]()
Solution

Binomial Denominators
Before we begin work on rationalizing the denominator of fractions which contain binomial expressions with radicals in them, let us look again at binomial multiplication. Consider the following examples:
![]()
![]()
![]()
Notice that in each of the above examples the answer does not contain any radicals, the answer is a rational number. Notice also that the expressions being multiplied have the form
a - b and a + b. You should recall that the product (a - b)(a + b) = a2 - b2. Also you should be able to see that a2 - b2 will always give a rational answer even when a and b themselves contain square roots.
The expressions a - b and a + b are said to be conjugates of each other. We will use this concept to rationalize the denominator of fractions in the following examples.
Example 1
Simplify (i.e. rationalize the denominator) : ![]()
Solution
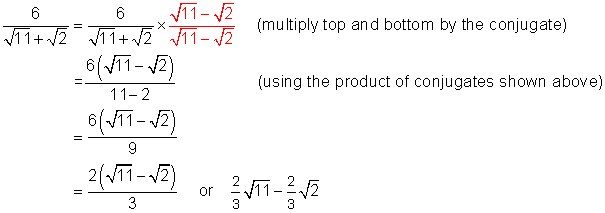
Example 2
Simplify: ![]()
Solution
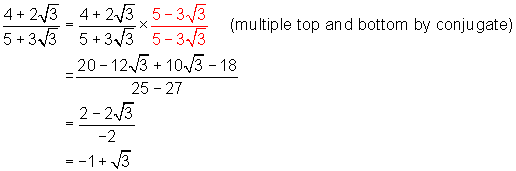
Example 3
Simplify: ![]()
Solution
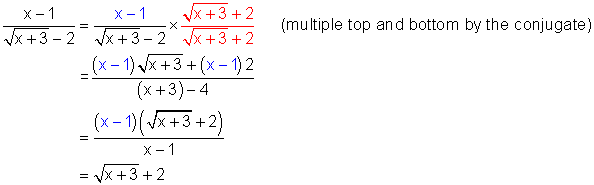
Example 4
Simplify: ![]()
Solution
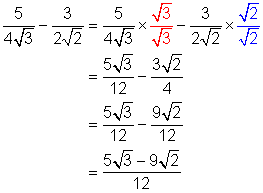
Example 5
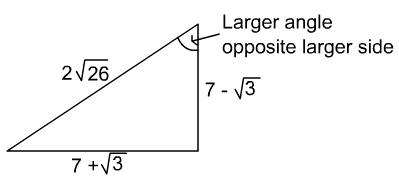
Find the secant of the larger acute angle in a right triangle with sides ![]()
Solution
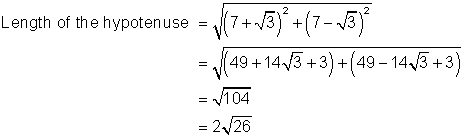
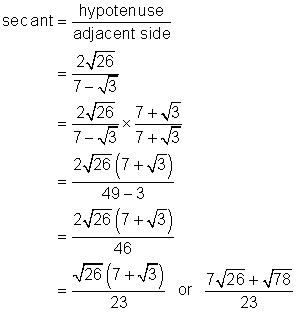
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
For questions 1 to 11, rationalize the denominator and simplify. Assume that all radicals denote real numbers.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]() 7.
7. 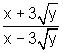 8.
8. ![]()
9. ![]() 10.
10. ![]() 11.
11. ![]()
12. The lengths of the legs of a right triangle are ![]() and
and ![]() units long. Find the ratio of the hypotenuse to the longer leg. Relative to the smaller acute angle, which trigonometric ratio have you found?
units long. Find the ratio of the hypotenuse to the longer leg. Relative to the smaller acute angle, which trigonometric ratio have you found?
Test Yourself
For questions 1 to 9, rationalize the denominator and express the answer in simplest radical form.
1. ![]() 2.
2. ![]() 3.
3. ![]()
4. ![]() 5.
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]() 9.
9. ![]()
10. What is the slope of the line passing through the points ![]() ?
?
Express your answer in simplest radical form.