Learning Resources

Home »  » Courses » Mathematics » Mathematics 3103 (delisted) » Unit 02 » Set 02 ILO 04 » Go to Work

Lesson

Like Radicals

Two radicals are said to be like radicals if they have the same index and radicand.

Consider the following examples:

                     Unlike Radicals                                   Why

                                            different radicands

                                             different indexes

 

                       Like Radicals                                    Why

                                                 Each pair has

                                                the same index
                                                                                        and

                                     the same radicand

To simplify sums and differences of radicals:

1. Express each radical in simplest form.
2. Combine terms in which the radicals have the same index and radicand (i.e. are like radicals).

Example 1

Simplify: 

Solution

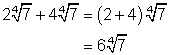                                      ( Note the similarity to 2x + 4x)

 

Example 2

Simplify:    

Solution

                           

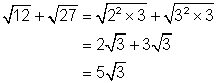
Example 3

Simplify:  

Solution

                             

 

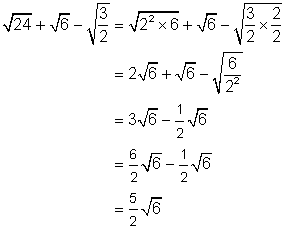
Example 4

Simplify:  

Solution

               

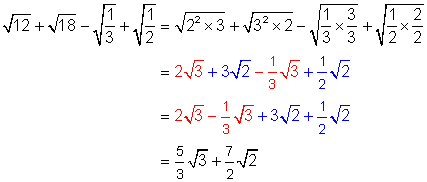
Application to Multiplying Binomials

You learned to multiply binomial expressions in previous courses. To do so you probably used the distributive property as shown below:

(x -2)(2x + 1) = x(2x + 1) - 2(2x + 1) = x(2x) + x(1) -2(2x) -2(1) = 2x² - 3x - 2

You may also have learned the acronym FOIL (standing for First, Outside, Inside, Last) as a memory trick to help you remember the order of multiplication.

Example 1 below is a review of the process of multiplying binomials. If you do not like the FOIL acronym, just apply the distributive property in your usual way.

Example 1

Multiply:   (2x - 3)(5x + 4)

Solution:

                                                     F             O             I              L
                   (2x - 3)(5x + 4) = (2x)(5x) + (2x)(4) + (-3)(5x) + (-3)(4)
                                            = 10x² + 8x - 15x - 12
                                            = 10x² - 7x - 12

Note in this example you combined the like terms, viz. 8x and  -15x

We are going to apply this same technique to multiplying binomials which contain radicals. In short we are substituting irrational numbers in the form of radicals for the variable. This is shown in the following examples.

Example 2

Simplify:  

Solution

             

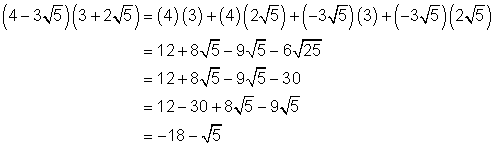
Example 3

Simplify:   

Solution

              

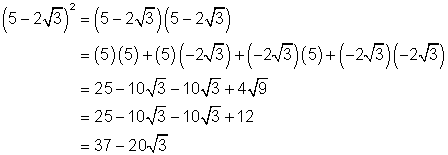
Example 4

Simplify:  

Solution

      

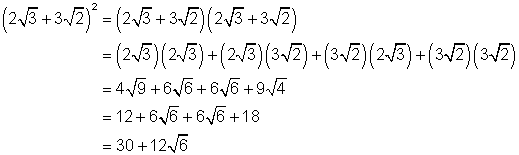
Note: You can check the above multiplications by using your calculator. Simply enter the given expression and then enter the answer you get when you simplify. Both answers should give the same approximation.

Activity

Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.

For each of the following, perform the indicated operations and write your answer in simplest radical form.

1.                                 2. 

3.                                           4.  

5.                         6.  

7.                                   8.  

9.                          10.  

11.                                      12.  

Answers

Test Yourself

In each of the following, perform the indicated operations and write your answer in simplest radical form.

1.                          2.                       3.     

4.                         5.                    6. 

7.              8.  

9.                  10. 

Answers