
Learning Resources
Lesson
Rule #1
A radical with index n is in simplest form when the radicand contains no factor (other than 1) that is the nth power of an integer or polynomial.
To apply this rule, first factor the radicand and express the factors in exponential form with exponents that are multiples of the index of the radical.
Example 1
Simplify: ![]()
Solution
Example 2
Simplify (assume the given radical denotes a real number) ![]()
Solution
Example 3
Simplify (assume the given radical denotes a real number) ![]()
Solution
We have worked with the rules for multiplication and division of radicals in an earlier lesson. Another rule or property that is useful for simplification is the power of a root property. It states:
If ![]() is a real number, then
is a real number, then ![]()
The following example shows this property applied in connection with the rule for simplification stated above.
Example 4
Simplify: ![]()
Solution
Rule #2
A radical is in simplest form when the radicand does not contain:
1. a fraction
2. a negative exponent.
To apply this rule you must use your knowledge of equivalent fractions to rewrite the fraction under the radical with a denominator for which the root can be found. You must also use your knowledge of negative exponents and rewrite any expression with a negative exponent as a fraction.
Example 1
Simplify: 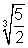
Solution
Example 2
Simplify: ![]() where a > o
where a > o
Solution
Example 3
Simplify: ![]()
Solution
Example 4
Simplify: ![]()
Solution
Rule #3
A radical is in simplest form when the index n is as small as possible.
To apply this law you need the root of a root property. It states:
If each radical denotes a real number, then ![]()
You can apply this rule whenever the index of the radical and the exponent of the radicand contain a common factor and the index is larger than the exponent.
Example 1
Simplify: ![]()
Solution
Example 2
Simplify: ![]()
Solution
Rule #3 will be a lot easier for you to apply when you learn the relation between radicals and exponents in a later chapter. For that reason little else is done with it in this lesson.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Simplify the following. Assume each radical represents a real nth root and that each denominator is not zero.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]() 7.
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. 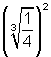 11.
11. ![]() 12.
12. ![]()
Test Yourself
Simplify the following. Assume each radical represents a real nth root and that each denominator is not zero.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]() 7.
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()