Learning Resources
Lesson
Multiplication
Consider the following examples:
and 
and 
Although a few particular examples do not constitute a proof, nevertheless they do suggest a pattern. In fact, both of these examples demonstrate the following rule for the product of radicals:
Let 
and 
be any real nth root. Then,
Examples
1. 
2. 
3. 
We can use this rule for multiplication in reverse to "simplify" the radical by removing a factor from the radicand for which the root can be found. We can use this process to make the radicand the smallest positive integer possible. This is shown in the following examples.
Examples
4. 
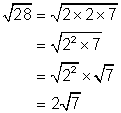
5. 
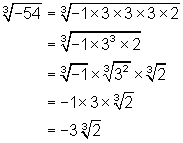
Pay particular attention to the way the index is written in Example 5 above. If you are sloppy over your notation, expressions like 
(three times the square root of two) and 
(the cube root of two) become indistinguishable. The index is always smaller and raised above the base of the radicand.
6. 
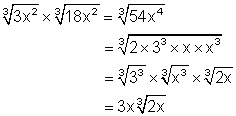
The whole technique of simplifying radicals will be discussed at a much greater length in the next lesson. For now concentrate on the rule for multiplying radicals and learn to apply it both ways.
Division
Consider the following examples:
and 
and 
Note: there are certain numbers for which you should know the square root without having to write them in exponential form or use a calculator. These include 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 225, 400, 625. Similarly, there are certain numbers for which you should know the cube root. These include 8, 27, 64, 125, 216, 343, 512, 1000. The examples above assume you know these values.
Both of the examples above suggest the following rule for the quotient of radicals:
Let and be any real nth root. Then,
Examples
1. 
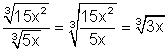
2. 
3. 
Note: In the above examples the denominators were always numbers for which the root could be found. When the denominator is not a number for which the root can be found, we multiply to make it so. This process is known as rationalizing the denominator and it will be dealt with in much more detail in a later lesson. For now the following example will suffice to demonstrate the concept:
4. 
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Multiply or divide as indicated:
1. 
2. 
3. 
4. 
5. 
6. 
Use the rules for multiplication and division of radicals to change the form of each of the following so that the radicand is the smallest integer possible.
7. 
8. 
9. 
10. 
11. 
12. 
Test Yourself
Multiply or divide as indicated:
1. 
2. 
3. 
4. 
5. 
6. 
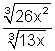
Use the rules for multiplication and division of radicals to change the form of each of the following so that the radicand is the smallest integer possible.
7. 
8. 
9. 
10. 
11. 
12. 