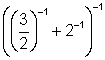Learning Resources
Lesson
Laws and Examples
The laws which follow are true for all integers m and n and all non-zero real numbers a and b.
Law 1: To multiply powers of the same base you add the exponents:
am x an = am + n
Before we look at examples of the application of this law consider why it appears to be true by considering the following: 32 x 33 = (3 x 3) x (3 x 3 x 3) = 3 x 3 x 3 x 3 x 3 = 35
Examples: 34 x 3-5 = 3-1 = ![]() ;
; ![]() ;
; ![]()
Law 2: To divide powers of the same base you subtract the exponents:
![]()
Again, before we look at examples of the application of this law consider why it appears to be true by considering the following: ![]()
Examples: ![]() ;
; ![]() ;
; ![]()
Law 3: To raise a power to a power you multiply the exponents:
![]()
Before we look at examples of the application of this law consider why it appears to be true by considering the following: ![]()
Examples: ![]() ;
; ![]() ;
; 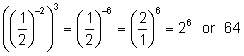
Law 4: The power of a product is equal to the product of the powers:
![]()
Before we look at examples of the application of this law consider why it appears to be true by considering the following: 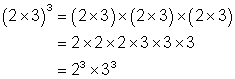
Examples: ![]() ;
; ![]() ;
; ![]()
Law 5: The power of a quotient is equal to the quotient of the powers:
![]()
Again, before we look at examples of the application of this law consider why it appears to be true by considering the following: 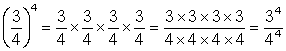
Examples: ![]() ;
; 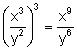 ;
; 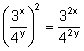
The next page of this lesson contains several examples showing how these laws can be applied to simplifying more complex expressions.
Application to Simplifying Expressions
Example 1
Simplify the following expression and write the answer with positive exponents only:
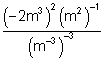
Solution
Example 2
Simplify the following expression and write the answer with positive exponents only:
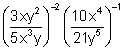
Solution
Example 3
Express each number as a power of 2 and then simplify:
![]()
Solution
Example 4
Simplify the following expression and write the answer with positive exponents only:
![]()
Solution
Now go to the Activities section and complete the exercises there.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Simplify the following. Do not leave any negative exponents.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. 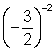 6.
6. ![]() 7.
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. 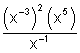 11.
11. 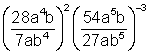 12.
12. 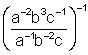
Express each term in the following expression as a power of three and then simplify:
13. ![]()
Test Yourself
Simplify the following. Express results without negative or zero exponents.
1. ![]() 2.
2. 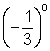 3.
3. ![]() 4.
4. 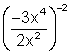
5. 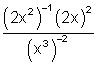 6.
6. 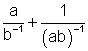 7.
7. ![]() 8.
8. ![]()
9. 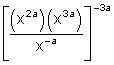 10.
10. ![]() 11.
11. 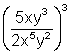 12.
12.