Learning Resources
Lesson
Defining Zero Exponents
In previous grades you learned the Law of Exponents for division of powers to the same base. It said that when a > b , 
. We would like this law to also apply when a = b. Thus for example we would get:
and 
But you learned in a much earlier grade that any number (other than zero) divided by itself is one. Thus
and 
From the above, we can see that it is reasonable to conclude that 30 = 1 and 20 = 1. These examples suggest a definition for zero exponents.
Definition: If x is any nonzero real number, x0 = 1
The following examples show how this definition is applied:
50 = 1 ; 
; ( 5 - 2)0 = 1 ; (x + 3)0 = 1 ;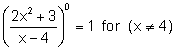 
Defining Negative Exponents
In addition to the Law of exponents stated above for a > b, you also learned that when a < b , 
. We wish these two laws for division of exponents to apply regardless of the values of a and b. Thus for example we would get:
and 
also 
and 
From the above, we can see that it is reasonable to conclude that 
and that 
. These examples suggest a definition for negative exponents.
Definition: if x is any nonzero real number, 
The following examples show how this definition is applied:
; 
; 
From the definition and the examples above we can see that, x-n is the reciprocal of xn .
Consider the following example:
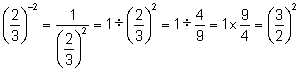
This example suggests the following generalization to the definition of negative exponents when it is applied to fractional expressions:
Remembering this application of the definition of negative exponents can save time when simplifying expressions later in this unit. For example:
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
Express each of the following in simplest form without exponents:
1. 4-1 2. 02 3. 
4. 
5. 
6. 3-5 x 35 7. 8-1 x 30 8. 
9. 
10. 
11. 
12. 
Simplify and express only with positive exponents:
13. 
14. 
15. 
16. 
Test Yourself
Express each of the following in simplest form without exponents:
1. 
2. 2-3 3. 
4. 5-2 x 60
5. 4-1(7 - 4)0 6. (1 + 2)-3 7. 
8. 
9. 
10. 
11. 
12. 3-1 + 2-1
Simplify and express only with positive exponents:
13. 
14. 