Review
Assigned activities
Section 01 The Real Number System (answers)
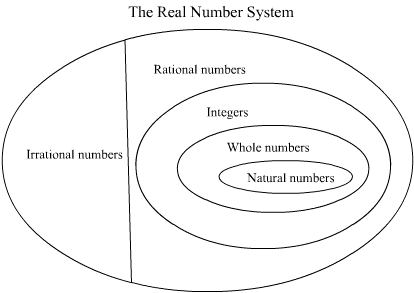
- The real number system, its various subsets, and the relation
between them is shown the diagram below. We can use it to help
answer the questions in this problem:
(a)
3 is natural, whole, integer, rational, real
(b)
-3 is integer, rational, real
(c)
2.5 is rational, real
(d)
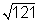( another name for 11) is natural, whole, integer, rational, real
(e)
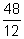 (another
name for 4) is natural, whole, integer, rational, real
(f)
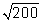 is
irrational (a non repeating, non terminating decimal), real
(g)
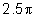 is
irrational, real
(h) 4.52
is rational, real
-
(a) He may sell no shoes at all, so smallest number is 0.
(b) The whole numbers describe the number of pairs since he can't
sell
part of a pair or a negative number
of pairs.
(c) {x | x ³ 0 where x Î
Whole numbers}.
(d) {x | x > 19 where x Î Whole
numbers}.
alternately {x | x ³
20 where x Î Whole numbers}.
(e) {x | x > 19 and x < 41 where x Î
Whole numbers} which can also
be written as {x | 19 < x < 41
where x Î Whole numbers} or
{x | 20 £
x £ 40
where x Î Whole numbers}
-
(a) Since she can't sell part of a suit, the set is the whole
numbers.
(b) Jane sells more than 3 and less than 21 suits. Alternately we
can
say she must sell between 3 and 21
suits. Mathematically we say:
{n | 3 < n < 21 where n Î
Whole numbers} or
{n | 4 £ n
£ 20 where n Î
Whole numbers}
(c) Jane earns no less than $60 (4 x $15) and no more than $300
(4 x $15). Mathematically we can say:
{y | $60 £
y £ $300, where y Î
Whole numbers}
-
(a) Equivalent
(b) Equivalent
(c) Not equivalent
(d) Not equivalent
|
