
Learning Resources
Lesson
Equations Involving Percentages
To solve equations involving percentages first convert the percentage to a decimal or a fraction and then proceed in the usual fashion. This is shown in the examples below.
Example 1
Solve for x: x + 12% of 22 = 3.7
Solution
Example 2
Solve for x: 5.2 + 18% of x = 9.7
Solution
Example 3
Solve for x: 8.2 + x% of 12.4 = 10.432
Solution
Example 4
Solve for x: x + 24% of x = 43.4
Solution
Using Percentages in Problem Situations
Example 1
Consumer reports rate a particular model of new car to have an average depreciation rate of 20%. If you pay $28 000 for this car when it is new, what is:
- the dollar amount of depreciation in the first year?
- the car value after the first year?
- the dollar amount of depreciation in the second year?
- the car value after the second year?
- if you sell the car after 5 years, what would you expect to get for it?
Solution
Example 2
A car salesman receives a base salary of $250 per month plus 1.5% commission on the value of automobiles sold. In a particular month his gross salary was $2 320. What was the value of his sales for the month?
Solution
Example 3
A winter coat is advertised as 40% off. At the checkout you are asked to pay $103.50, which included the 15% HST. What was the original price of the coat?
Solution
Note that in the preceding example we multiplied by 115% instead of finding 15% and adding it on. This is a technique you can use to increase any quantity by any given percent. Since the original is always 100%, if we add on x% you get (100 + x)%, and (100 + x)% of a number is that number multiplied by (100 + x)%. For example, to increase 75 by 20% we simply have to multiply 75 by 1.2 ; to increase 7000 by 5% we multiply by 1.05 .
Percentages and Graphs of Growth and Decay
Example 1
There were originally (time = 0) 100 bacteria in a laboratory culture. After one hour (time = 1) there were 120 and after 2 hours (time = 2) there were 144.
- What was the percentage increase each hour?
- Assuming this percentage increase remains constant, use a spreadsheet or some other technology to determine the number present at the end of each hour for a 24 hour period.
- Draw a graph of the data using the hour number as the domain and the number of bacteria as the range.
- From the graph, estimate to the nearest hour how long it took the bacteria to become ten times its original size.
Solution
(a) Number increase first hour = 120 - 100 = 20
Percentage increase first hour = 20/100 =20%
Number increase second hour = 144 - 120 = 24
Percentage increase second hour = 24/120 = 20%
Percentage increase each hour is 20%
(b) Since the percentage increase remains constant at 20%, we can find the number present at the end of any given hour by multiplying the number present the previous hour by 120%. For example:
Number present after 3 hours = 120% of 144 = 172.8
The table below shows this process for a 24 hour period:
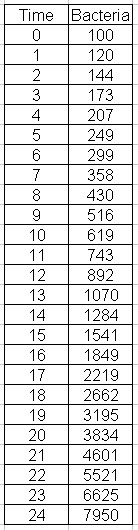
(c) 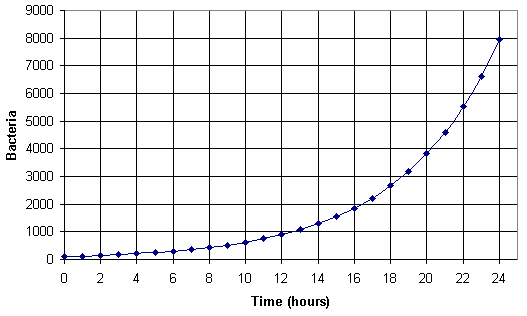
(d) The original number was 100. Ten times the original would be 1000. Draw a line across from 1000 on the y-axis and read the x-coordinate where it intersects the graph. To the nearest hour, it is 13. To see this line click "show" on the graph below.
Example 2
A country currently (year = 0) has 500 000 hectares of forest which are disappearing at the rate of 5% every 10 years.
- Assuming this percentage decrease remains constant, use a spreadsheet or some other technology to determine the area present at the end
of each 10 year period for 200 years. - Draw a graph of the data using the 10 year number as the domain and the forest area as the range.
- From the graph, estimate how long it will take for the area to be half its current size.
- If the forest continues to disappear at the same rate, will the country ever
completely run out of forest area?
Solution
(a) Since the decrease is 5%, that means there is 95% left at the end of each ten year period.
Original area = 500 000 hectares
Area after first 10 years = 95% of 500 000 = 475 000 hectares
Area after second 10 years (i.e. after 20 years) = 95% of 475 000
= 451 250 hectares
The values in the table below are obtained by continuing this process.
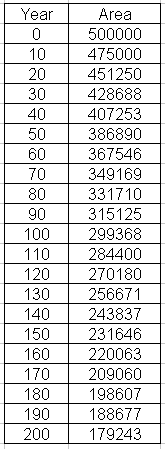
(b) 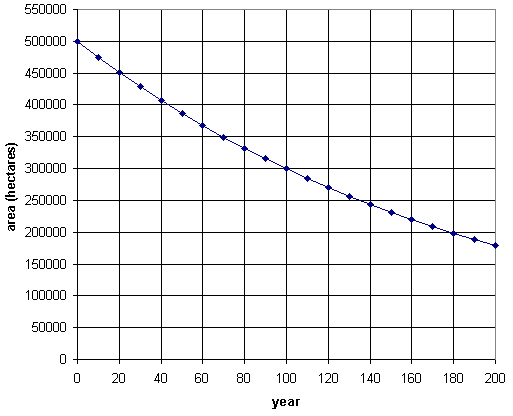
(c) Original area = 500 000 hectares
Half this area = 250 000 hectares
Draw a line across from 250 000 on the y-axis and read the x-coordinate
where it intersects the graph. To the nearest year, it is 135. To see this
line click "show" on the graph below.
(d) From a theoretical point of view, the value of the forest area will never reach zero because we are always taking 95% of some positive number. The graph will never cross or touch the x-axis. However, from a practical point of view, the forest area would eventually be reduced so small as to be an unusable area.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Solve each of the following for x:
(a) x + 25% of 40 = 10% of 95
(b) 22 + 30% of x = 64
(c) x% of 42 - 12.3 = 4.5
(d) x - 35% of x = 58.5 - An item which has an original sticker price of $90 was discounted by 35%.
(a) What is the sale price before tax?
(b) What percentage of the original price is this sale price?
(c) What is the price after 15% HST has been added?
(d) By what percentage can you multiply the price of any item to get the final price including the 15% HST?
(e) What percentage of the original sticker price is the price including tax? - (a) What is 30% of 40% of 80?
(b) By what one percentage could you multiply 80 to get the answer in (a)? - Brian bought a new computer for $1500. After one year it was worth $1050, after two years it was worth $735.
(a) What is the annual rate of depreciation?
(b) If he sells the computer after five years, what should be the asking price? - When Ted was born (time = 0) his grandfather invested $5000 in a term deposit that compounded yearly. On Ted's first birthday (t = 1) the investment had a value of $5500, and on Ted's second birthday (t = 2) it had a value of $6050.
(a) What was his yearly rate of interest?
(b) Use a spreadsheet or some other technology to determine the value of the investment on Ted's 21st birthday.
(c) Draw a graph of the data using the year number as the domain and the value of the investment as the range.
(d) For those wishing a challenge, calculate the value of the investment on Ted's 50th birthday.
Test Yourself
- Solve each of the following for x:
(a) x = 45% of 30 + 30% of 45
(b) 48% of x = 1.2
(c) x% of 210 = 58.8
(d) x = 63.8 - 45% of x
- You start a new job which gives you two options: Option A offers a starting salary of $400 per week with a guaranteed increase of 3% per year; Option B offers a starting salary of $350 per week with a guaranteed increase of 10% per year.
(a) Which offer is better if you plan to work at the job for 3 years? Explain.
(b) Which offer is better if you plan to work at the job for 6 years? Explain.
- A person has a job which pays a base wage of $250 per week plus 4% commission on total sales. If the person received a check showing a gross amount of $400, what were his total sales for the week?
- Jack initially (year = 0) invested $5000 in a 20 year term deposit with a guaranteed interest rate which compounded yearly. At the end of the first year his investment had a value of $5550 and at the end of the second year his investment was valued at $6160.50.
(a) What was his yearly rate of interest?
(b) Use a spreadsheet or some other technology to determine the value of the investment at the end of each year for the 20 year period.
(c) Draw a graph of the data using the year number as the domain and the value of the investment as the range.
(d) How long will it take the investment to double in value?