Learning Resources
Lesson
Multiplying and Dividing with Decimals
When multiplying two numbers which contain decimals, the number of digits after the decimal point in the answer is equal to the sum of the number of digits after the decimal points in the two numbers. For example,
5.3 x 0.002 will have 4 digits after the decimal in the answer.
Thus to multiply these numbers mentally, ignore the decimal points and multiply 53 x 2 to get 106. Then insert the decimal point so 4 digits are after it; this gives 0.0106 .
Similarly,
0.04 X 2.1 will have 3 digits after the decimal point in the answer.
To multiply these numbers mentally, multiply 4 X 21 to get 84. Then insert the decimal point so 3 digits are after it; this gives 0.084 .
When dividing by a number that contains a decimal, first make the divisor a whole number by multiplying by the appropriate power of ten. Thus, if the divisor is 0.056 we would multiply by 1000 to make it 56; if the divisor is 1.53 we would multiply by 100 to make it 153.
Recall that multiplying by a power of ten simply moves the decimal point the number of places to the right corresponding to the exponent in the power of ten. For example, multiplying by 10 (= 101) moves it one place, by 100 (=102) moves it two places, etc.
Recall also that if you multiply the divisor by a power of ten (i.e. move the decimal point), you must also multiply the dividend by the corresponding power of ten to have an equivalent expression. This is shown in the following example.
Example 1
12.46 ¸ 0.002
Solution
We can short cut the process simply by moving the decimal in both the divisor and the dividend the required number of places as shown below:
Rounding
Rounding is the process of making an approximation to a given number by using fewer significant figures. Essentially it involves dropping digits after a certain significant place. The rules for rounding are described below.
When the first digit dropped is less than 5, the preceding digit is not changed. For example (digit to be dropped is in red):
45.649 rounded to the tenth's place is 45.6
4713.6 rounded to the ten's place is 4710
Notice in the second example above the importance of 0 as a place holder.
When the first digit dropped is greater than 5, the preceding digit is increased by 1. For example (digit to be dropped is in red):
45.669 rounded to the tenth's place is 45.7
4717.6 rounded to the ten's place is 4720
When the digit to be dropped is equal to 5, we have to be more cautious. In fact, there is not total agreement about the rule among the various branches of the sciences. However, the following rules are generally accepted by most:
If the digit dropped is 5 followed by some succeeding non-zero digits, the preceding digit is increased by 1. For example,
3.685012 rounded to the hundredth's place is 3.69
If the digit dropped is 5 followed only by zeros, the commonly accepted rule (used by computers) is to:
increase the preceding digit by 1 if it is odd
leave the preceding digit unchanged if it is even
For example,
47.8350 rounded to the hundredths place is 47.84
47.8650 rounded to the hundredths place is 47.86
Converting Fractions to Decimals and Percents
To convert a fraction to a decimal, simply divide the denominator into the numerator.
Example 1
Write each of the following as a decimal (do NOT use a calculator to help):
(a) 
(b) 
Solution
(a)
(b)
To convert a fraction to a percent, you can proceed two ways. First, since a percent is only a fraction with a denominator of 100, you can use the technique of writing equivalent fractions. We simply replace the denominator of 100 by %, the percent symbol. This is shown in Example 2(a) below.
Example 2
Write each of the following as a percent: (a) (b)
Solution
(a)
Notice that an alternative to the above solution could have been to first convert the fraction to a decimal. Then multiply the resulting decimal by 100 and write the % sign after it. Thus:
= 0.925 = 0.925 x 100% = 92.5%
(b) = 0.72 = 0.72 x 100% = 72.2%
Converting Percents to Decimals and Fractions
Recall that the symbol for percent, viz. %, means 1/100 or 0.01 . Thus, to convert a percent to a decimal simply divide by 100 or multiply by 0.01. For example:
13% = 13 ¸ 100 = 0.13
3.5% = 3.5 ¸ 100 = 0.035
135% = 135 ¸ 100 = 1.35
To convert a percent (which does not contain repeating digits after the decimal) to a fraction, write the percent as a fraction with a denominator of 100 (as noted above % means 1/100). Then reduce the fraction to lowest terms. For example:
28% = 
7.8% = 
To convert a percent which contains repeating digits after the decimal point refer to page 5 of this lesson.
Converting Decimals to Fractions and Percents
To convert a terminating decimal to a fraction, write all the significant digits from the decimal form as the numerator of the fraction; write a power of 10 as the denominator 10 (=101), 100 (=102), 1000 (= 103), etc. where the exponent in the power of 10 equals the number of digits after the decimal point in the original decimal form of the number. This is shown in the two examples below.
Example 1
Example 2
To convert a terminating decimal to a percent, multiply by 100 and insert the % sign. Using the two examples above we get:
0.732 = 0.732 x 100% = 73.2%
3.46 = 3.46 x 100% = 346%
To convert a repeating decimal to a percent is the same procedure as for a terminating decimal, viz. multiply by 100. For example:
0.76 = 0.76 x 100% = 76.6%
1.527 = 1.527 x 100% =152.727%
There are several methods you can use to convert a repeating decimal to a fraction. One method is shown in the example below.
Example 3
Convert 0.45 to a fraction.
Solution
Example 4
Convert 0.123 to a fraction.
Solution
Ordering and Place Value
To order decimal numbers, compare the digits in each of the successive place values. To see how this works let's consider the example from the Pre-Test.
Example
Match each number with the correct position on the given number line:
4.89; 4.35; 4.9; 4.16; 4.375; 4.49; 4.65; 4.515; 4.2131549
Solution:
The numbers are all the same in the units place, so compare the digits in the tenth's place. The smallest tenth's place digit is 1, hence 4.16 is the smallest number and it must match with point A.
The next smallest tenth's place digit is 2, hence 4.2131549 is the next smallest number and it must match with point J.
The numbers 4.35 and 4.375 each have a tenth's place digit of 3, so we have to compare their hundredth's place digits. The smaller hundredth's place digit is 5, hence 4.35 is smaller and matches with point B. The other number, 4.375 therefore matches with point C.
You can continue this process to match all the remaining numbers to the points on the line.
The matching of certain points with certain numbers should be obvious for other reasons. For example, 4.49 is a little less than half the interval between 4 and 5, and 4.51 is a little greater than half. Obviously the two points that must match with them are D and E respectively.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Calculate each of the following mentally:
(a) 1.34 x .02 (b) 0.11 x 0.11 (c) 0.009 x 80
(d) -24 ¸ (-300) (e) 600 ¸ 0.06 (f) -9 ¸ 0.03 - Round each number as indicated:
(a) 34.76 to the tenth's place
(b) 473.82 to the ten's place
(c) 0.014501 to the thousandth's place
(d) 16500 to the thousand's place
(e) 2.475 to the hundredth's place - Put the following set of numbers in order from smallest to largest:
2.51; 2.49; 2.5123; 2.49; 2.51; 2.49; 2.51
- Do the following mentally:
(a) Express 0.12 as (i) a percent, (ii) as a fraction in lowest terms
(b) Express 5.25% as a decimal
(c) Express 8% as (i) a decimal, (ii) a fraction in lowest terms
(d) Express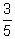
as (i) a decimal, (ii) a percent - (a) Express
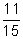as (i) a decimal, (ii) a percent
(b) Express 8.75% as (i) a decimal, (ii) a fraction in lowest terms
(c) Express 0.0124 as (i) a percent, (ii) a fraction in lowest terms
(d) Express 0.124 as (i) a percent, (ii) a fraction in lowest terms.
Test Yourself
- Perform the following calculations mentally. Do not use pencil and paper or calculators to help.
(a) -0.2 x 1.6 (b) 21 ¸ 0.007 (c) 4.76 ¸ 0.001 - Round each of the following numbers as indicated:
(a) 791.43 to the nearest (i) tenth, (ii) hundred
(b) 3596 to the nearest (i) ten, (ii) thousand
(c) 0.0651 to the nearest hundredth
(d) 2.0685 to the nearest thousandth
(e) 6.75 to the nearest tenth - Convert each of the following as indicated. Do whatever you can mentally and use pencil and paper for the rest. Do not use a calculator.
(a)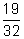
to (i) a decimal, (ii) a percent
(b)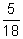
to (i) a decimal, (ii) a percent
(c) 0.36% to (i) a decimal, (ii) a fraction (in lowest terms)
(d) 0.48 to (i) a fraction (in lowest terms), (ii) a percent
(e) 0.325 to (i) a fraction (in lowest terms), (ii) a percent -
Put the following numbers in order from smallest to largest:
1.692; 1.69; 1.69; 1.69; 1.6973; 1.692