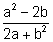Learning Resources
Lesson
Simplification of Complex fractions
A complex fraction is defined to be a fraction in which the numerator and/or denominator are themselves fractions.
There are several methods that may be used to simplify complex fractions. Three of them are shown below using the same example for comparison. Pick the one you prefer and be sure you understand it. The same method used for numerical fractions will be used extensively in another unit of this course dealing with algebraic fractions or rational expressions.
Example 1
Simplify: 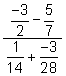
Method 1
In this method you first rewrite the complex fraction as a division problem and apply the skills you learned in the previous lessons.
Method 2
This method is very similar to the previous one, except you leave the fraction in complex form and only change to a division problem near the end.
Method 3
In this method you first find the LCD of ALL the fractions in the complex fraction and then multiply the numerator and denominator by this LCD. Since you are multiplying the numerator and denominator of the complex fraction by the same number, the new fraction will be equivalent to the original one. However it will be much simpler.
Example 2
Simplify: 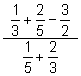
Solution
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Simplify each of the following complex fractions. Try to do the work mentally, without using pencil and paper or technology:
(a)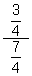 (b)
(b) 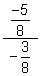 (c)
(c) 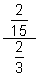 (d)
(d) 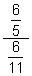
(e)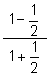 (f)
(f) 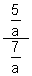
- Simplify:
(a)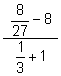 (b)
(b) 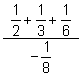 (c)
(c) 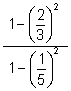 (d)
(d) 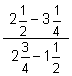
- If a = -
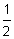 and b =
and b = 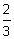 , evaluate:
, evaluate:
(a)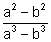 (b)
(b) 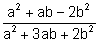
Test Yourself
- Try to simplify the following complex fractions mentally:
(a)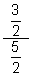 (b)
(b) 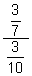 (c)
(c) 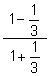
- Simplify:
(a)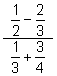 (b)
(b) 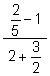 (c)
(c) 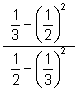
- If a =
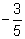 and b =
and b = 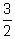 , evaluate
, evaluate