
Learning Resources
Lesson
Multiplication and Division Algorithms
To multiply two fractions together, we multiply the numerators together and the denominators together using the algorithm shown below:
![]()
For example: ![]() .
.
However, if we apply this algorithm directly, quite often the the fraction that results from the multiplication is not in lowest terms and has to be reduced down. This is shown in the following example: ![]()
To avoid this, we can divide any common factors that may exist in the numerator and denominator at the start, before we multiply using the algorithm. Applying this to the above example we would get:
This short cut technique of dividing common factors into the numerator and denominator (note we are not canceling or crossing off anything) can be most beneficial with more complex fractions. However, you must remember that what we divide must be a factor. This will be critical when we deal with algebraic fractions like ![]() in a later unit. The temptation is to "cross off" the x, but x is not a factor, and hence we cannot divide the numerator and denominator by it. As noted above, we will discuss this more in a later unit.
in a later unit. The temptation is to "cross off" the x, but x is not a factor, and hence we cannot divide the numerator and denominator by it. As noted above, we will discuss this more in a later unit.
Example
Multiply ![]()
Solution
There are several approaches that can be taken for developing an algorithm for division of fractions. One is shown in the example below:
We can now combine the skills for addition, subtraction, multiplication, and division to do more complex examples like the one below:
Example
Simplify: ![]()
Solution
Example
Simplify: ![]()
Solution
Applications to Graphs
In earlier courses you learned how to generate graphs from a table of values. Usually the table contained integer values or decimals, but many patterns for graphs are generated using fractions as well. This is illustrated in the following example.
Example
Start with the number 2 (call it step 0). Divide this number by ![]() (call it step 1). Then divide the result in step 1 by
(call it step 1). Then divide the result in step 1 by ![]() (call it step 2); then divide the result in step 2 by
(call it step 2); then divide the result in step 2 by ![]() (call it step 3); etc.
(call it step 3); etc.
- Set up a table of at least 7 values and use it to plot the points on a graph. Use the step numbers as the x-coordinate and the results of the calculations as the y-coordinate.
- Describe the shape of the graph.
- Give the domain and range of the graph.
Solution
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Multiply or divide as indicated. Do whatever problems you can mentally. Do the rest using pencil and paper. Do not use technology (calculators, etc.) to help you do these problems:
(a)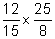 (b)
(b) 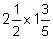 (c)
(c) 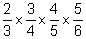
(d)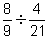 (e)
(e) 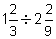 (f)
(f) 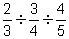
(g)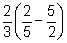 (h)
(h) 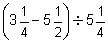 (i)
(i) 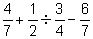
(j)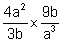
- A person bought shares in the stack market valued at $1 per share (year = 0). At the end of the first year the value of the stock was
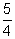 times its initial value. At the end of the second year it was
times its initial value. At the end of the second year it was 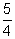 times what it was at the end of the first year. This trend was consistent throughout each day of the year and continued to the end of the sixth year.
times what it was at the end of the first year. This trend was consistent throughout each day of the year and continued to the end of the sixth year.
(a) Without using a calculator, construct a table of values showing the stock value at the end of each of the six years. Express all amounts as mixed fractions.
(b) Use the table to construct a graph of the stock value verses time.
(c) What is the domain and range of the graph?
(d) Use the graph to estimate the stock value at the end of 4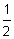 years.
years.
Test Yourself
- Multiply or divide as indicated. You should be able to do these problems mentally.
(a)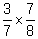 (b)
(b) 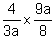 (c)
(c) 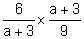
(d)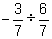 (e)
(e) 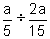
- Perform the indicated operations:
(a)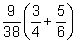 (b)
(b) 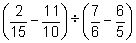 (c)
(c) 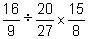
(d)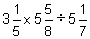
- Start with the number 9 (call it step 0). Take
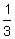 of this number (call it step 1). Then take
of this number (call it step 1). Then take 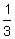 of the result in step 1 (call it step 2); then
of the result in step 1 (call it step 2); then 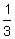 of the result in step 2 (call it step 3); etc.
of the result in step 2 (call it step 3); etc.
(a) Set up a table of values of at least 7 points and use them to plot the graph using the step numbers as the x-coordinate and the results of your calculations as the y-coordinate. Leave answers in fractional form. Do not use a calculator to approximate.
(b) Will the graph ever intersect or go below the x-axis?. Explain.
(c) State the domain and range of the graph.