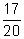Learning Resources
Lesson
Lowest Terms
A fraction is in lowest or simplest terms when there are no common factors in the numerator and denominator.
To reduce a fraction to lowest terms you can divide the numerator and denominator by the greatest common factor. One way to do this is to find all the prime factors of the numerator and denominator and then divide out the ones that are common. The two fractions are equivalent, that is they name the same number.
A technique for reducing to lowest terms is shown in the following examples:
Example 1
Reduce to lowest terms: ![]()
Solution
Example 2
Reduce to lowest terms: ![]()
Solution
The same technique can be applied to fractions which contain algebraic expressions. We will deal more with this in Unit 4 of this course. The following example will show you how to work with fractions which contain numbers can be applied directly to fractions which contain algebraic expressions.
Example 3
Reduce to lowest terms: ![]()
Solution
Lowest Common Denominator
When we work with fractions it is sometimes necessary to express them with the same or common denominator. Furthermore, it is easiest if this common denominator is as small as possible. Finding the Least Common Denominator (LCD) of two or more fractions is especially useful when adding and subtracting fractions, a topic that will be discussed in the next lesson of this section.
To find the least common denominator, we find the least common multiple of the denominators. To do this we write the prime factorization of each of the denominators and use it to select the factors necessary to form the least common multiple. This is shown in the examples below.
Example 1
Find the LCD of these fractions: ![]() and
and ![]()
Solution
Example 2
Find the LCD of these fractions: ![]() ,
, ![]() ,
, ![]()
Solution
The relative size of two or more fractions can sometimes be determined by inspection. For example, when comparing the fractions ![]() ,
, ![]() , and
, and ![]() , it is obvious that
, it is obvious that ![]() is a little less than
is a little less than ![]() , that
, that ![]() is a little greater than
is a little greater than ![]() , and that
, and that ![]() is greater than 1. It is thus very easy to put them in order of size.
is greater than 1. It is thus very easy to put them in order of size.
However, sometimes it may be necessary to first find the LCD and then express each of the fractions as its equivalent fraction using the LCD. This is shown in the following example.
Example 3
Which fraction is smaller ![]() or
or ![]() ?
?
Solution
Improper Fractions and Mixed Numbers
A proper fraction is a fraction in which the numerator is smaller than the denominator, e.g. ![]() ,
, ![]() .
.
An improper fraction is a fraction in which the numerator is greater than the denominator, e.g. ![]() ,
, ![]() .
.
A mixed number is a number expressed as the sum of a whole number and a proper fraction, e.g. 3 + ![]() which is shortened to 3
which is shortened to 3![]() .
.
Any improper fraction can be expressed as a mixed number and vice versa. The examples below show how each of the conversions may be performed.
Example 1
Express as mixed numbers: (a) ![]() , (b)
, (b) ![]()
Solution (a)
Solution (b)
Example 2
Express as improper fractions: (a) ![]() , (b)
, (b) ![]()
Solution (a)
Solution (a) Shortcut Method
There is a short cut method that can be used for converting from mixed numbers to improper fractions. It is shown in the steps below.
Solution (b)
Since ![]() can be written as
can be written as ![]() , we can work with the fraction inside the bracket and simply retain the negative in the answer. Both the basic definition and the shortcut method are shown in the steps below.
, we can work with the fraction inside the bracket and simply retain the negative in the answer. Both the basic definition and the shortcut method are shown in the steps below.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Reduce the following fractions to lowest terms:
(a)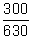 (b)
(b) 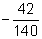
- Find the LCD of the following fractions:
(a)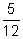 ,
,  ,
, 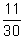 (b)
(b) 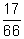 ,
, 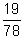 ,
, 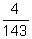
- Convert to a mixed number:
(a)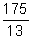 (b)
(b) 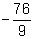
- Convert to an improper fraction:
(a)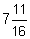 (b)
(b) 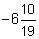
- Place the following fractions in order from smallest to largest:
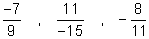
Test Yourself
Try to do the calculations for questions 1 to 5 mentally. The others may require pencil and paper.
- Reduce to lowest terms:
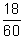
- Find the LCD of these fractions:
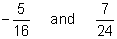
- Convert to a mixed number:
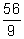
- Convert to an improper fraction:
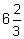
- Put the following fractions in order from smaller to larger:
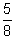 ,
, 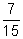
- Reduce to lowest terms:
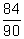
- Find the LCD of these fractions:
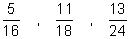
- Convert to a mixed number:
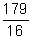
- Convert to an improper fraction:
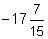
- Put the following fractions in order from smallest to largest:
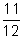 ,
, 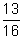 ,
,