Learning Resources

Home »  » Courses » Mathematics » Mathematics 3103 (delisted) » Unit 01 » Set 01 ILO 02 » Go to Work

Lesson

Applications of the Subsets

Before we look at applications of the real numbers and its various subsets, let's look once again at the definitions of each of the sets.

Natural numbers = {1 , 2, 3, 4, 5, . . .}

Whole numbers = { 0, 1, 2, 3, 4, . . .}

Integers = { . . . . -3, -2, -1, 0, 1, 2, 3 , . . .}

Rational numbers = = {terminating and repeating decimals}

Irrational numbers = {non-repeating infinite decimal}

Real numbers = {rational numbers, irrational numbers}

When you read through a problem, keep these definitions in mind and try to determine which of them will contain ALL the possible values for a given quantity in the problem.

Ask yourself the following questions about the quantities involved:

• Can all the values be named by counting?
• Can the value ever be zero?
• Do the values include negative numbers?
• Can the value of the quantity involved be a decimal value?
• Can the value under consideration ever be a radical value?

Each of the questions from the pre-test is discussed below. If you have not read them, click on the You Will Button above and do so before you proceed.

Question 1(a)

We are talking about the number of pop cans that a person returns for recycling. We assume that you cannot return part of a can. The number system that defines the number of cans is the natural or counting numbers (unless you allow the possibility of not recycling any cans, then the set is the set of whole numbers).

An interesting spin on the recycling problem would be if you were being paid by the weight of the metal in the can. Then it would be possible to use any amount of metal from a can and be paid for it. You could have 6.7 kg of metal, or 56.3 kg, or any positive decimal quantity limited only by the precision of the scales being used. Then the number system would be the positive real numbers (positive since the weight cannot be negative).

Question 1(b)

The Pythagorean Theorem tells us that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the two sides. Thus if the hypotenuse is c, and the sides are a and b respectively, then:

Notice that we are dealing with radicals. You know from the previous lesson that a radical may be either rational (like ) or an irrational (like ). Since the number can be either rational or irrational we are dealing with the real numbers. However, since the length of a segment cannot be negative we are dealing only with the positive real numbers.

Question 1(c)

Since the thermometer can only record temperatures to the nearest degree, we cannot have temperatures like 3.2 °C. The temperatures recorded by this thermometer can be positive or negative, but cannot contain decimals (to nearest degree). We are thus dealing with the set of integers.

Question 1(d)

In this question we are dealing with a ratio of wins to games played. A ratio is a number of the form , and in this case a is the number of wins and b is the number of games played. The value of a could be 0, 1, 2, 3, ... and the value of b could be 1, 2, 3, ... (assuming the team has played at least one game). The ratio is thus zero or some positive rational number. Thus we can say the set of non-negative rational numbers contains all possible ratios that can be generated by this problem.

Domain and Range

You learned in earlier mathematics courses that the domain is the set of all possible values of the independent variable and the range is the set of all possible values of the dependent variable.

To name either the domain or range completely requires stating both the set of numbers from which the values are taken and any restrictions that might be place on each. For example, consider the function:

If we are to stay in the real number system, the value of x must not be negative. We can thus state the domain of this function as:

Domain = {x | x ³ 0, x Î }

This is read as: "the domain is the set of all values of x such that x is greater than or equal to zero and x belongs to the real number system.

We can apply this same concept to stating the domain and range of variables when the variables are in problem situations. This is shown by discussing the questions from the pre-test dealing with this concept.

Question 2

The problem tells us that the switch only has a precision that allows recording temperatures to the nearest degree. Thus no decimal quantities are possible. For example, a real temperature of 3.2567 ºC is recorded, displayed, and acted on as though it was 3 ºC.

We know that the temperatures can be positive , negative , or zero. This, combined with the fact that we cannot use decimals, means that the values of the variable that represents temperature must come from the set of integers.

Next consider the restrictions. The heating system will not cut in as long as the temperature is 20 ºC or higher. If we let t represent the temperature, the values of t for which the heating system is off can be written using the following mathematical notation:

System off = {t | t ³ 20, t Î I}

The heating system will be on for all temperatures below 20 ºC. The value of t for which the heating system is on can be written using the following mathematical notation:

System on = {t | t < 20, t Î I}

Note that since t belongs to the set of integers, the above inequality can also be written as:

System on = {t | t £ 19, t Î I}

Question 3

The key to part (a) is the word proportion. To determine a proportion requires a fraction, e.g. 1/2, 3/4, 2/5,etc. Each of these numbers can of course be expressed as a percent, e.g. 50%, 75%, 40% (we will learn more about this in a future lesson). Furthermore, we know that there are no negative numbers, but she may decide not to work at all, thus zero is a possibility. All the possible numbers she can use to describe the number of dresses cut out is thus taken from the set of positive rational numbers.

In part (b) we find that there is a restriction of a maximum of 5 hours (300 minutes) and that she can cut out one dress in 40 minutes. The maximum number of dresses she can cut out is thus 300/40 or 7.5. We know the minimum is zero if she decides not to work. The set of all possible number of dresses she can cut out thus falls between 0 and 7.5. If we let x represent the number of dresses, we can describe the domain for this problem mathematically as follows:

Domain = {x | 0 £ x £ 7.5, x Î }

For part (c) we use the relation that the amount of money she makes, y, is 10 times the number of dresses she makes. We can describe this relation mathematically as
y = $10x, and we can write the range as follows:

Range = {y | 0 £ y £ 75, y Î R }

Question 4

Graph 1 Graph 2

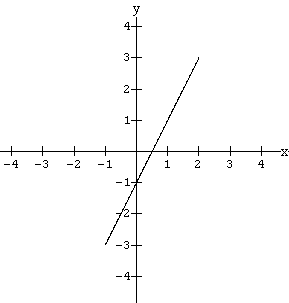
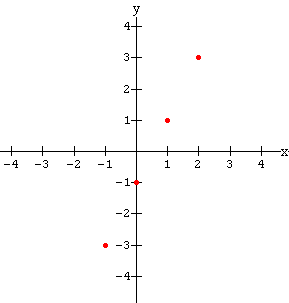
By inspection, it is obvious that the minimum and maximum value of x is the same on both graphs, viz. minimum -1 and maximum 2. This means that the inequality for the domain of the relation described by these graphs looks the same. The difference is in the numbers that exist between the maximum and minimum. Graph 1 is a solid line which indicates that all the real numbers are involved. However, Graph 2 is a set of distinct points; for example, there is no point between (-1 , -3) and (0 , -1). The two inequalities that describe the domains are thus:

Domain (graph 1) = {x | -1 £ x £ 2, where x Î R}
Domain (graph 2) = {x | -1 £ x £ 2, where x Î I}

We read this notation as: "The set of all x such that -1 is less than x, and x is less than 2".

You should see now why it is necessary to specify the set of numbers from which x is chosen. The inequality part of the domain definition is the same for both graphs, but the graphs are clearly not the same. It is the second part of the definition, the "where x Î I" and "where x Î R" that is critical for complete definition of the domain.

Similarly, the inequalities that describe the range of the two graphs are the same except for the part which tells which number system is being used. Thus we have:

Range (graph 1) = {y | -3 £ y £ 3, where y Î R}

Range (graph 2) = {y | -3 £ y £ 3, where y Î I}

Activity

Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.

1. Bill sells cars at Used Cars R-US
   (a) What is the smallest number of cars he can sell each week?
   (b) Which set of numbers would describe the number of cars sold?
   (c) If n represents the number of cars sold, combine your answers to (a) and (b) to write an inequality expressing the restriction on the number of cars sold.
   (d) Bill's boss feels that Bill could be selling more cars, so he introduces a performance quota that states Bill must sell at least 4 cars each week.
   Revise your inequality in (c) to reflect this new situation.
   (e) Bill knows that based on his past experience he cannot expect to sell any more than 25 cars, even in his best week. Revise your inequality in (d) to reflect this new situation.

2. Derek writes articles for the Downhomer magazine. He gets paid $250 for each article he writes.
   (a) What set of numbers can be used to describe the number of articles he can write?
   (b) The magazine requires a minimum of 5 and a maximum of 24 articles per year. If n represents the number of articles he submits, write a sentence and a mathematical inequality to describe the number of articles Derek is allowed to submit each year.
   (c) If y represents the amount of money he earns, write a sentence and an inequality showing the range of the amount of money he can earn.

3. As a part time job, Nadine baby sits for her neighbors. She is paid $6.00 per hour and is paid for any part of an hour she works. For example, if she works 20 minutes she gets paid for 20/60 or 1/3 of an hour, which is $2.00. She never works more than 40 hours per week.
   (a) If h represents the number of hours she works in one week, write an inequality showing all the possible number of hours she can work. Be sure to include the set of numbers used.
   (b) What is the minimum and maximum amount of money that Nadine can earn in a week?
   (c) If y represents the amount of money she earns in one week, write an inequality showing all the possible amounts she can earn.
   (d) Suppose another stipulation was that Nadine had to work a minimum of 8 hours per week. Write an inequality for the new domain and range of the problem.

4. For turkeys over 6 kilograms, the cooking time is 5.2 hours plus 0.25 hours per kilogram. If k represents the weight of the turkey and t the time, this relation can be expressed using the equation t = 0.25k + 5.2.
   (a) Write an inequality for the domain of this relation.
   (b) Write an inequality for the range of this relation.
   (c) Revise the inequalities in (a) and (b) to show that the relation only holds for turkeys less than 18 kilograms.

Answers

Test Yourself

Heather cuts material to make couches for Spinney Manufacturing. She is paid $13.50 for each complete bundle she cuts. She is required to cut at least 7 complete bundles per week.

1. If she gets nothing for partially cut bundles, write an inequality for the number of all possible couch bundles Heather can cut each week. What set of numbers did you use and why?
2. Heather and a group of other workers complained to the company that they should get paid for partially cut bundles; for example, if they cut 1/2 a bundle they should get paid 1/2 of $13.50 or $6.75. The company eventually agreed to this scheme. Revise your inequality in (1) to reflect this new situation.
3. If E represents the amount of money earned by Heather in a week, write an inequality to show the restrictions on E.
4. Because of her home commitments, Heather will work a maximum of 5 hours per day and 4 days per week. It takes her 30 minutes to cut one complete couch bundle.
   (a) If T is the amount of time Heather works each week, write an inequality to show the restrictions on T.
   (b) Revise your inequality in (2) to show the possible number of couch bundles she can cut.
   (c) Revise your inequality in (3) to show the possible amounts of money she can earn in one week.

Answers