Learning Resources
Lesson
Natural and Whole Numbers
The set of natural numbers is {1 , 2 , 3 , 4 , 5, ....}. These are the numbers that we use for counting and they are sometimes called counting numbers. We call them natural numbers because they are the ones most naturally invented by man. Even primitive peoples invented natural numbers.
A natural number is used as a cardinal number when it describes how many things are in a set (for example, 15 people in your mathematics 3103 course). A natural number is used as an ordinal number when it marks the position of something in a sequence (for example, the car in position 3 in an auto race).
A natural number does not have to be written using one of the numerals 1, 2, 3, 4, ... to be a natural number. For example 
and 
are both natural numbers because 
and 
.
The relationship of the natural numbers to the other subsets of the real numbers is shown in the Venn Diagram below:
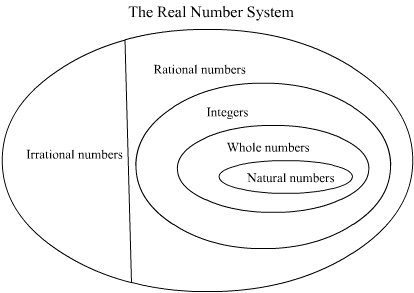
From the diagram, we can see that any natural number is also a whole number, an integer, a rational number, and a real number. Note however that a natural number is not an irrational number. If you want to learn more about these other number systems, refer to the other pages in this lesson.
The different number systems evolved in response to questions that could not be answered using the then current set of numbers. Thus, using only natural numbers there was no way of expressing the absence of any number. For example, there is no natural number for the number of students in Level III who are less than 2 years old. To describe that number we need the concept of the number zero.
Similarly the natural numbers cannot be used to answer the question "How many students are in attendance in a class of 5 if 5 of them are home sick?". For these types of questions another number system is needed. It is called the whole number system.
The set of whole numbers consists of the set of natural numbers plus zero. Thus the set of whole numbers is {0, 1, 2, 3, 4, 5, ...}. The description of the natural numbers provided above thus applies to the whole numbers. In addition to the natural numbers, the whole numbers also contain the number zero.
In the Venn Diagram above, the only number inside the whole number region and outside the natural number region is zero.
Integers
There are many questions and situations that cannot be handled using only the whole numbers. For example, "If the current temperature is 11 °C and the temperature drops 15 °C, what is the new temperature?". To answer this question requires another system of numbers. This set of numbers is called the set of integers.
A concept associated with any number system is that of the additive inverse. The additive inverse of a given number is the number that must be added to it to give zero. Thus, if 4 + x = 0, we say that x is the additive inverse of 4. The additive inverse of 4 is written as -4 and we know that -4 + 4 = 0. Clearly there are no additive inverses in the system of whole numbers. This again points to the necessity of having a number system other than the whole numbers.
The set of integers consists of the set of whole numbers plus their additive inverses. The set of integers is { . . . , -3, -2, -2, -1, 0, 1, 2, 3, 4, . . . }. Note that an integer can be named using symbols other than the numerals . . . -2, -1, 0, 1, 2, . . . For example, 
and are both integers because 
and .
The Venn diagram below shows the relation between the set of integers and the other subsets of the real numbers.
Note that the set of integers is a subset of the rational numbers and the real numbers. That is, all integers are also rational and real.
Note also that the set of integers contains the whole numbers and the natural numbers as subsets. Thus all whole numbers and natural numbers are also integers.
The numbers inside the set of integers but outside the set of whole numbers are numbers like -3, -245, etc.
Rational Numbers
There are many questions and situations that cannot be handled using the set of integers. For example, how do you quantify a temperature that is somewhere between 4 °C and 5 °C , or how do you share $20 evenly among 8 people?
To answer these and similar questions you need a number system that extends beyond the integers. That system is the set of rational numbers.
A rational number is any number that can be named by a fraction that has integers for its numerator and denominator, but the denominator cannot be zero. A rational number is thus any number that can be expressed as an integer or as the quotient of integers. The following are some examples:
, 
, 
or 
, 
or 
,
The letter Q is often used to name the set of rational numbers since a rational number can always be expressed as the quotient of two integers.
Since any rational number is the quotient 
of two integers, where b ¹ 0, it can be renamed as a decimal by dividing a by b. For example:
, 
, 
, 
The results above are written as repeating decimals, using bars to show which digits repeat. If the only repeating digit is 0, as in the first example, the decimal is also called a terminating decimal because we can (and usually do) write it without the 0.
From the above discussion, you can see that another definition that is sometimes given for a rational number is that it is any number that can be written as a repeating or terminating decimal. Fractions and decimals (repeating and terminating) are thus only two different forms that can be used to express a given rational number.
The natural numbers, the whole numbers and the integers are subsets of the rational numbers, since any of them can be expressed as the quotient of two integers (one way is simply to let the denominator equal 1). The relation between the rational numbers and these other sets is shown in the Venn Diagram below.
Note that there are still some real numbers that cannot be expressed using the rational numbers. These are called the irrational numbers and are described on page 4 of this lesson.
The rational and irrational numbers together form the set of real numbers. If a number is real it must be either a rational or irrational number. There are numbers that are neither rational nor irrational; that is, they are not real. We will discuss these in a later unit of this course.
Irrational Numbers
There are many questions and situations that cannot be handled using the set of rational numbers. For example, suppose we wish to find a number which when multiplied by itself gives 10. Algebraically this question can be considered as the solution to the equation:
or 
There is no rational number to solve this equation. The solution is the square root of 10, which is denoted by the expression 
. The ± sign denotes that there are two square roots of 10. If you use your calculator to get a decimal approximation for to 9 places after the decimal you see that it is 3.162277660. This decimal does not repeat nor does it terminate.
In fact the square root of any non perfect square number cannot be expressed as a repeating or terminating decimal. That is, it cannot be expressed as the ratio of two integers and hence is not a rational number. Such numbers are examples of irrational numbers.
An irrational number is a number that cannot be expressed as a ratio of two integers. In the decimal form, an irrational number appears as a non-repeating infinite decimal.
Note that all radicals are not irrational numbers. For example 
is a rational number because it is another representation for the number 7. Similarly 
is rational because it is another representation for - 3.5, which is a terminating decimal and hence a rational number.
There are many other irrational numbers besides the square roots of non perfect square integers. One such number that most people are familiar with is the number p. Even in ancient times, people knew that for any circle the ratio of the circumference to the diameter was a value slightly greater than 3. Around 1700 B.C. , the Egyptians used the fraction 
to approximate the ratio, while Greeks of about 22 B.C. used 
to approximate it. It was the Greeks that used their letter p to represent the exact value of the ratio. The Chinese, Hindu, and Europeans all developed their own approximations for the ratio of the circumference to the diameter, but in 1761 Johann Lambert proved there is no rational number equal to p .
The relationship between the irrational numbers and the other subsets of the real numbers is shown in the diagram below.
Note that if a number is irrational it cannot also belong to the rational numbers or any of its subsets.
The rational and irrational numbers together form the set of real numbers. If a number is real it must be either a rational or irrational number. There are numbers that are neither rational nor irrational; that is, they are not real. We will discuss these in a later section of this course.
Activity
Print off a copy of this page and add it to your Math 3103 binder. Then answer the questions in your binder.
- Can a number be both rational and irrational? Explain your answer with the help of a diagram.
- Which set of the real numbers does not contain any other numbers?
- What other sets are contained by the:
- rational numbers
- whole numbers
- irrational numbers
- natural numbers
- integers
- Classify each of the numbers below according to ALL the subsets of the real numbers to which it belongs:
(a)  |
(b)  |
(c)  |
(d)  |
|
| (e) 5.23 | (f) 5.23 | (g) 5.23p | (h)  |
Test Yourself
Classify each of the following numbers according to ALL the subsets of the real numbers to which it belongs, i.e. tell if the number is a natural number, a whole number, an integer, a rational number, an irrational number, a real number.
| (a) 7 | (b) -36 | (c)  |
(d)  |
| (e) 6.735 | (f) - |
(g) 2p | (h) -3.6 |